To create a template of the required task you should use the PT4Load tool (starting with version 4.22, you can use the PT4Panel tool for quick launch of all Programming Taskbook tools; the PT4Panel shortcut is located on the desktop and in any working directory).

The created template is located in the working directory and consists of several files and subdirectories. But we need only the Begin3.rb file for Ruby and the Begin3.jl file for Julia. This file will be loaded into the code editor of VS Code or RubyMine IDE:

[Ruby]

# coding: utf-8
require "./PT"

def solve()
    task "Begin3"

end

start_solve

[Julia]

include("PT.jl")

function solve()
    task("Begin3")

end

start_solve()

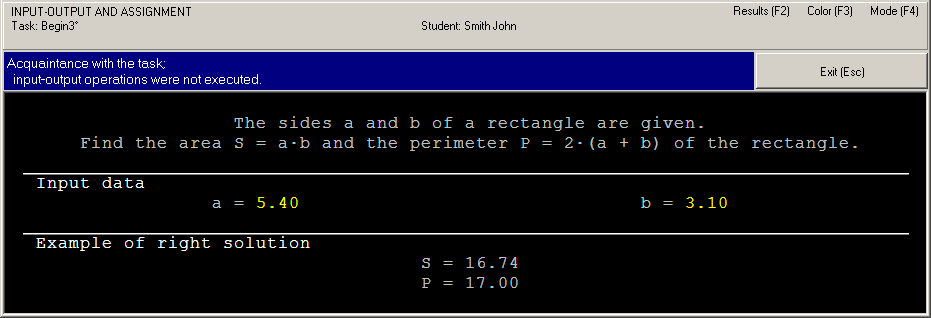
The Begin3 file contains definition of the solve function that already contains the task function call that initializes the Begin3 task. The solution of the task should be entered in the solve function (of course any other functions may be used).

To run the program, press [F5] (for VS Code) or [Shift]+[F10] (for RubyMine). When the program is launched, you will see the Programming Task window with a task text and initial data.

This running is considered as acquaintance running because the program does not perform input-output operations. To close the Programming Taskbook window click the Exit button or press [Esc] or [F5] (for VS Code) or [F10] (for RubyMine).

Initial data input

Before solving tasks, you should input initial data in the program. In the Begin3 task, the initial data are real numbers a and b that refer to sides of the rectangle.

There are two functions that provide input of the real numbers: the get function and the get_f function. The get_f function also checks type of the current data item and output error message if the type of data item differs from the Float type. Let's use the get_f function (we show the solve function only):

[Ruby]

def solve()
    task "Begin3"
    a = get_f
    b = get_f
end

[Julia]

function solve()
    task("Begin3")
    a = get_f()
    b = get_f()
end

Run the program once again. You will see the new set of initial data. For each running of the program a new initial data are generated, so it is necessary to develop an algorithm that processes correctly all admissible sets of initial data.

Data input is performed correctly, but the program does not output results. In such situation, we have the following message: "Correct data input: all required data are input, no data are output" (Programming Taskbook version 4.15 or higher) or "Some data are not output" (previous versions).

Calculation and output results

Let's perform the required calculations and output results using the put function:

[Ruby]

def solve()
    task "Begin3"
    a = get_f
    b = get_f
    p = 2 * (a + b)
    s = a * b
    put P, S
end

[Julia]

function solve()
    task("Begin3")
    a = get_f()
    b = get_f()
    p = 2 * (a + b)
    s = a * b
    put(P, S)
end

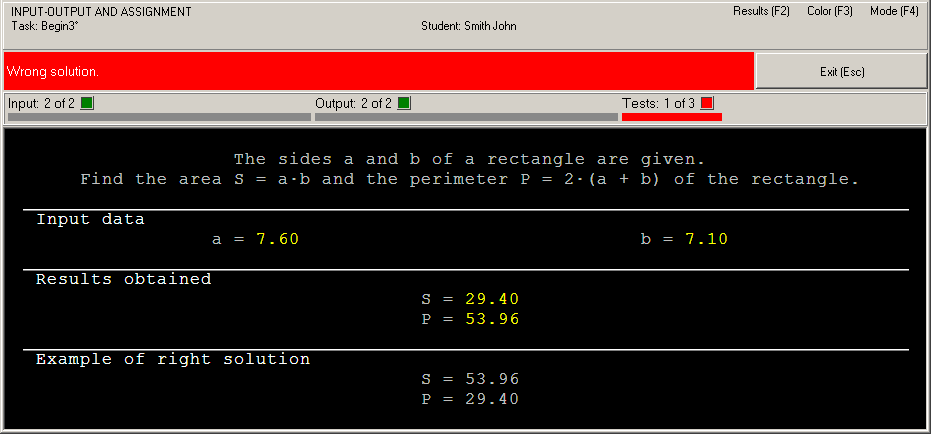
In this case, the running leads to the following information in the status bar: "Error NameError: uninitialized constant P" (for Ruby) or "UndefVarError: P not defined" (for Julia).

To correct the program, it is enough to change its last statement as follows:

[Ruby]

    put p, s

[Julia]

    put(p, s)

When the program is running, you can see output values at the panel of results. Because we output data in inverse order, the status bar contains the error message "Wrong solution".

Right solution and its testing

To correct the last error, it is enough to change order of two parameters of the put function:

[Ruby]

    put s, p

[Julia]

    put(s, p)

When this program is running, you will see the testing panel on screen:

This panel appears when the program processes successfully at least one set of input data. The progress bar shows the amount of tests which are already performed, the text above the bar allows to determine how much tests should be performed successfully. The program testing finishes in two cases: when all required tests are performed successfully or when some test is failed.

In our case, the algorithm is correct, therefore the message "The task is solved!" will be shown.

To browse information about the task solving, you can use PT4Results tool (you may run this tool by pressing the [F2] key or clicking the Results label in the upper-right corner of the Programming Taskbook window):

Begin3      r23/02 20:13 Acquaintance with the task.
Begin3      r04/02 15:07 Correct data input.
Begin3      r04/02 15:09 Error NameError.
Begin3      r04/02 15:12 Wrong solution.
Begin3      r04/02 15:15 The task is solved!

The letter "r" denotes the programming language (Ruby); the letter "u" is used for Julia.

Remark. It is not necessary to use additional variables s and p, because you can output expressions. You can also use the get function instead of the get_f one and use the "parallel" assignment:

[Ruby]

def solve()
    task "Begin3"
    a, b = get, get
    put a * b, 2 * (a + b)
end

[Julia]

function solve()
    task("Begin3")
    a, b = get(), get()
    put(a * b, 2 * (a + b))
end

Starting from version 4.22, functions get2, get3, get4, get5 are available that return 2, 3, 4 or 5 consecutive elements of the input data (the elements can be of different types):

[Ruby]

    a, b = get2

[Julia]

    a, b = get2()

In Ruby, we can also use the put methods without parameters as followa:

[Ruby]

def solve()
  task "Begin3"
  a, b = get2
  (a * b).put
  (2 * (a + b)).put
end

Last revised:
01.01.2024