Process groups and communicators
Creation of new communicators
MPI5Comm1°. A sequence of K integers is given in the master process; K is the number of processes whose rank is an even number (0, 2, …). Create a new communicator that contains all even-rank processes using the MPI_Comm_group, MPI_Group_incl, and MPI_Comm_create functions. Send one given integer to each even-rank process (including the master process) using one collective operation with the created communicator. Output received integer in each even-rank process.
MPI5Comm2°. Two real numbers are given in each process whose rank is an odd number (1, 3, …). Create a new communicator that contains all odd-rank processes using the MPI_Comm_group, MPI_Group_excl, and MPI_Comm_create functions. Send all given numbers to each odd-rank process using one collective operation with the created communicator. Output received numbers in each odd-rank process in ascending order of ranks of sending processes (including numbers received from itself).
MPI5Comm3°. Three integers are given in each process whose rank is a multiple of 3 (including the master process). Using the MPI_Comm_split function, create a new communicator that contains all processes with ranks that are a multiple of 3. Send all given numbers to master process using one collective operation with the created communicator. Output received integers in the master process in ascending order of ranks of sending processes (including integers received from the master process). Note. When calling the MPI_Comm_split function in processes that are not required to include in the new communicator, one should specify the constant MPI_UNDEFINED as the color parameter.
MPI5Comm4°. A sequence of 3 real numbers is given in each process whose rank is an even number (including the master process). Find the minimal value among the elements of the given sequences with the same order number using a new communicator and one global reduction operation. Output received minimums in the master process. Note. See the note to MPI5Comm3.
MPI5Comm5°. A real number is given in each process. Using the MPI_Comm_split function and one global reduction operation, find the maximal value among the numbers given in the even-rank processes (including the master process) and the minimal value among the numbers given in the odd-rank processes. Output the maximal value in the process 0 and the minimal value in the process 1. Note. The program should contain a single MPI_Comm_split call, which creates the both required communicators (each for the corresponding group of processes).
MPI5Comm6°. An integer K and a sequence of K real numbers are given in the master process, an integer N is given in each slave process. The value of N is equal to 1 for some processes and is equal to 0 for others; the number of processes with N = 1 is equal to K. Send one real number from the master process to each slave process with N = 1 using the MPI_Comm_split function and one collective operation. Output the received numbers in these slave processes. Note. See the note to MPI5Comm3.
MPI5Comm7°. An integer N is given in each process; the value of N is equal to 1 for at least one process and is equal to 0 for others. Also a real number A is given in each process with N = 1. Send all numbers A to the first process with N = 1 using the MPI_Comm_split function and one collective operation. Output received numbers in this process in ascending order of ranks of sending processes (including the number received from this process). Note. See the note to MPI5Comm3.
MPI5Comm8°. An integer N is given in each process; the value of N is equal to 1 for at least one process and is equal to 0 for others. Also a real number A is given in each process with N = 1. Send all numbers A to the last process with N = 1 using the MPI_Comm_split function and one collective operation. Output received numbers in this process in ascending order of ranks of sending processes (including the number received from this process). Note. See the note to MPI5Comm3.
MPI5Comm9°. An integer N is given in each process; the value of N is equal to 1 for at least one process and is equal to 0 for others. Also a real number A is given in each process with N = 1. Send all numbers A to each process with N = 1 using the MPI_Comm_split function and one collective operation. Output received numbers in these processes in ascending order of ranks of sending processes (including the number received from itself). Note. See the note to MPI5Comm3.
MPI5Comm10°. An integer N is given in each process; the value of N is equal to 1 for some processes and is equal to 2 for others, there are at least one process with N = 1 and one process with N = 2. Also an integer A is given in each process. Using the MPI_Comm_split function and one collective operation, send integers A from all processes with N = 1 to each process with N = 1 and from all processes with N = 2 to each process with N = 2. Output received integers in each process in ascending order of ranks of sending processes (including the integer received from itself). Note. See the note to MPI5Comm5.
MPI5Comm11°. An integer N is given in each process; the value of N is equal to 1 for at least one process and is equal to 0 for others. Also a real number A is given in each process with N = 1. Find the sum of all real numbers A using the MPI_Comm_split function and one global reduction operation. Output the received sum in each process with N = 1. Note. See the note to MPI5Comm3.
MPI5Comm12°. An integer N is given in each process; the value of N is equal to 1 for some processes and is equal to 2 for others, there are at least one process with N = 1 and one process with N = 2. Also a real number A is given in each process. Using the MPI_Comm_split function and one global reduction operation, find the minimal value among the numbers A given in the processes with N = 1 and the maximal value among the numbers A given in the processes with N = 2. Output the minimal value in each process with N = 1 and the maximal value in each process with N = 2. Note. See the note to MPI5Comm5.
Virtual topologies
MPI5Comm13°. An integer N (> 1) is given in the master process; the number of processes K is assumed to be a multiple of N. Send the integer N to all processes and define a Cartesian topology for all processes as a (N × K/N) grid using the MPI_Cart_create function (ranks of processes should not be reordered). Find the process coordinates in the created topology using the MPI_Cart_coords function and output the process coordinates in each process.
MPI5Comm14°. An integer N (> 1) is given in the master process; the number N is not greater than the number of processes K. Send the integer N to all processes and define a Cartesian topology for the initial part of processes as a (N × K/N) grid using the MPI_Cart_create function (the symbol "/" denotes the operator of integer division, ranks of processes should not be reordered). Output the process coordinates in each process included in the Cartesian topology.
MPI5Comm15°. The number of processes K is an even number: K = 2N, N > 1. A real number A is given in the processes 0 and N. Define a Cartesian topology for all processes as a (2 × N) grid. Using the MPI_Cart_sub function, split this grid into two one-dimensional subgrids (namely, rows) such that the processes 0 and N were the master processes in these rows. Send the given number A from the master process of each row to each process of the same row using one collective operation. Output the received number in each process (including the processes 0 and N).
MPI5Comm16°. The number of processes K is an even number: K = 2N, N > 1. A real number A is given in the processes 0 and 1. Define a Cartesian topology for all processes as a (N × 2) grid. Using the MPI_Cart_sub function, split this grid into two one-dimensional subgrids (namely, columns) such that the processes 0 and 1 were the master processes in these columns. Send the given number A from the master process of each column to each process of the same column using one collective operation. Output the received number in each process (including the processes 0 and 1).
MPI5Comm17°. The number of processes K is a multiple of 3: K = 3N, N > 1. A sequence of N integers is given in the processes 0, N, and 2N. Define a Cartesian topology for all processes as a (3 × N) grid. Using the MPI_Cart_sub function, split this grid into three one-dimensional subgrids (namely, rows) such that the processes 0, N, and 2N were the master processes in these rows. Send one given integer from the master process of each row to each process of the same row using one collective operation. Output the received integer in each process (including the processes 0, N, and 2N).
MPI5Comm18°. The number of processes K is a multiple of 3: K = 3N, N > 1. A sequence of N integers is given in the processes 0, 1, and 2. Define a Cartesian topology for all processes as a (N × 3) grid. Using the MPI_Cart_sub function, split this grid into three one-dimensional subgrids (namely, columns) such that the processes 0, 1, and 2 were the master processes in these columns. Send one given integer from the master process of each column to each process of the same column using one collective operation. Output the received integer in each process (including the processes 0, 1, and 2).
MPI5Comm19°. The number of processes K is equal to 8 or 12. An integer is given in each process. Define a Cartesian topology for all processes as a three-dimensional (2 × 2 × K/4) grid (ranks of processes should not be reordered), which should be considered as 2 two-dimensional (2 × K/4) subgrids (namely, matrices) that contain processes with the identical first coordinate in the Cartesian topology. Split each matrix into two one-dimensional rows of processes. Send given integers from all processes of each row to the master process of the same row using one collective operation. Output received integers in the master process of each row (including integer received from itself).
MPI5Comm20°. The number of processes K is equal to 8 or 12. An integer is given in each process. Define a Cartesian topology for all processes as a three-dimensional (2 × 2 × K/4) grid (ranks of processes should not be reordered), which should be considered as K/4 two-dimensional (2 × 2) subgrids (namely, matrices) that contain processes with the identical third coordinate in the Cartesian topology. Split this grid into K/4 matrices of processes. Send given integers from all processes of each matrix to the master process of the same matrix using one collective operation. Output received integers in the master process of each matrix (including integer received from itself).
MPI5Comm21°. The number of processes K is equal to 8 or 12. A real number is given in each process. Define a Cartesian topology for all processes as a three-dimensional (2 × 2 × K/4) grid (ranks of processes should not be reordered), which should be considered as 2 two-dimensional (2 × K/4) subgrids (namely, matrices) that contain processes with the identical first coordinate in the Cartesian topology. Split each matrix into K/4 one-dimensional columns of processes. Using one global reduction operation, find the product of all numbers given in the processes of each column. Output the product in the master process of the corresponding column.
MPI5Comm22°. The number of processes K is equal to 8 or 12. A real number is given in each process. Define a Cartesian topology for all processes as a three-dimensional (2 × 2 × K/4) grid (ranks of processes should not be reordered), which should be considered as K/4 two-dimensional (2 × 2) subgrids (namely, matrices) that contain processes with the identical third coordinate in the Cartesian topology. Split this grid into K/4 matrices of processes. Using one global reduction operation, find the sum of all numbers given in the processes of each matrix. Output the sum in the master process of the corresponding matrix.
MPI5Comm23°. Positive integers M and N are given in the master process; the product of the numbers M and N is less than or equal to the number of processes. Also integers X and Y are given in each process whose rank is in the range 0 to M·N − 1. Send the numbers M and N to all processes and define a Cartesian topology for initial M·N processes as a two-dimensional (M × N) grid, which is periodic in the first dimension (ranks of processes should not be reordered). Using the MPI_Cart_rank function, output the rank of process with the coordinates X, Y (taking into account periodicity) in each process included in the Cartesian topology. Output −1 in the case of erroneous coordinates.
Note. If invalid coordinates are specified when calling the MPI_Cart_rank function (for instance, in the case of negative coordinates for non-periodic dimensions), then the function itself returns an error code (instead of the successful return code MPI_SUCCESS) whereas the return value of the rank parameter is undefined. So, in this task, the number −1 should be output when the MPI_Cart_rank function returns a value that differs from MPI_SUCCESS. To suppress the output of error messages in the debug section of the Programming Taskbook window, it is enough to set the special error handler named MPI_ERRORS_RETURN before calling a function that may be erroneous (use the MPI_Comm_set_errhandler function or, in MPI-1, the MPI_Errhandler_set function). When an error occurs in some function, this error handler performs no action except setting an error return value for this function. In MPICH version 1.2.5, the MPI_Cart_rank function returns the rank parameter equal to −1 when the process coordinates are invalid. This feature may sumplify the solution; however, in this case, one also should suppress the output of error messages by means of special error handler setting.
MPI5Comm24°. Positive integers M and N are given in the master process; the product of the numbers M and N is less than or equal to the number of processes. Also integers X and Y are given in each process whose rank is in the range 0 to M·N − 1. Send the numbers M and N to all processes and define a Cartesian topology for initial M·N processes as a two-dimensional (M × N) grid, which is periodic in the second dimension (ranks of processes should not be reordered). Using the MPI_Cart_rank function, output the rank of process with the coordinates X, Y (taking into account periodicity) in each process included in the Cartesian topology. Output −1 in the case of erroneous coordinates. Note. See the note to MPI5Comm23.
MPI5Comm25°. A real number is given in each slave process. Define a Cartesian topology for all processes as a one-dimensional grid. Using the MPI_Send and MPI_Recv functions, perform a shift of given data by step −1 (that is, the real number given in each process should be sent to the process of the previous rank). Ranks of source and destination process should be determined by means of the MPI_Cart_shift function. Output received data in each destination process.
MPI5Comm26°. The number of processes K is an even number: K = 2N, N > 1. A real number A is given in each process. Define a Cartesian topology for all processes as a two-dimensional (2 × N) grid (namely, matrix); ranks of processes should not be reordered. Using the MPI_Sendrecv function, perform a cyclic shift of data given in all processes of each row of the matrix by step 1 (that is, the number A should be sent from each process in the row, except the last process, to the next process in the same row and from the last process in the row to the first process in the same row). Ranks of source and destination process should be determined by means of the MPI_Cart_shift function. Output received data in each process.
MPI5Comm27°. The number of processes K is equal to 8 or 12. A real number A is given in each process. Define a Cartesian topology for all processes as a three-dimensional (2 × 2 × K/4) grid (ranks of processes should not be reordered), which should be considered as K/4 two-dimensional (2 × 2) subgrids (namely, matrices) that contain processes with the identical third coordinate in the Cartesian topology and are ordered by the value of this third coordinate. Using the MPI_Sendrecv_replace function, perform a cyclic shift of data given in all processes of each matrix by step 1 (that is, the numbers A should be sent from all processes of each matrix, except the last matrix, to the corresponding processes of the next matrix and from all processes of the last matrix to the corresponding processes of the first matrix). Ranks of source and destination process should be determined by means of the MPI_Cart_shift function. Output received data in each process.
MPI5Comm28°. The number of processes K is an odd number: K = 2N + 1 (1 < N < 5). An integer A is given in each process. Using the MPI_Graph_create function, define a graph topology for all processes as follows: the master process must be connected by edges to all odd-rank processes (that is, to the processes 1, 3, …, 2N − 1); each process of the rank R, where R is a positive even number (2, 4, …, 2N), must be connected by edge to the process of the rank R − 1. Thus, the graph represents N-beam star whose center is the master process, each star beam consists of two slave processes of ranks R and R + 1, and each odd-rank process R is adjacent to star center (namely, the master process). 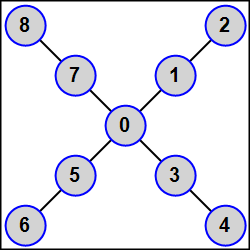
Using the MPI_Send and MPI_Recv functions, send the given integer A from each process to all its adjacent processes (its neighbors). The amount and ranks of neighbors should be determined by means of the MPI_Graph_neighbors_count and MPI_Graph_neighbors functions respectively. Output received data in each process in ascending order of ranks of sending processes.
MPI5Comm29°. The number of processes K is an even number: K = 2N (1 < N < 6). An integer A is given in each process. Using the MPI_Graph_create function, define a graph topology for all processes as follows: all even-rank processes (including the master process) are linked in a chain 0 — 2 — 4 — 6 — … — (2N − 2); each process with odd rank R (1, 3, …, 2N − 1) is connected by edge to the process with the rank R − 1. Thus, each odd-rank process has a single neighbor, the first and the last even-rank processes have two neighbors, and other even-rank processes (the "inner" ones) have three neighbors. 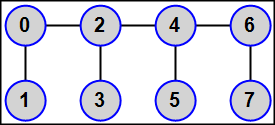
Using the MPI_Sendrecv function, send the given integer A from each process to all its neighbors. The amount and ranks of neighbors should be determined by means of the MPI_Graph_neighbors_count and MPI_Graph_neighbors functions respectively. Output received data in each process in ascending order of ranks of sending processes.
MPI5Comm30°. The number of processes K is equal to 3N + 1 (1 < N < 5). An integer A is given in each process. Using the MPI_Graph_create function, define a graph topology for all processes as follows: processes of ranks R, R + 1, R + 2, where R = 1, 4, 7, …, are linked by edges and, moreover, each process whose rank is positive and is a multiple of 3 (that is, the process 3, 6, …) is connected by edge to the master process. Thus, the graph represents N-beam star whose center is the master process, each star beam consists of three linked slave processes, and each slave process with rank that is a multiple of 3 is adjacent to star center (namely, the master process). 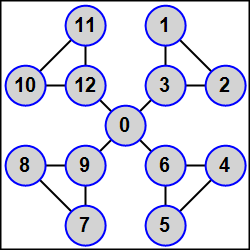
Using the MPI_Sendrecv function, send the given integer A from each process to all its neighbors. The amount and ranks of neighbors should be determined by means of the MPI_Graph_neighbors_count and MPI_Graph_neighbors functions respectively. Output received data in each process in ascending order of ranks of sending processes.
The distributed graph topology (MPI-2)
MPI5Comm31°. The number of processes K is a multiple of 3; an integer A is given in each process. Using the MPI_Dist_graph_create function, define a distributed graph topology for all processes as follows: all processes whose rank is a multiple of 3 (0, 3, …, K − 3) are linked in a ring, each process in this ring is the source for the next process of the ring (that is, the process 0 is the source for the process 3, the process 3 is the source for the process 6, …, the process K − 3 is the source for the process 0); besides, the process 3N (N = 0, 1, …, K/3 − 1) is the source for the processes 3N + 1 and 3N + 2, and the process 3N + 1 is the source for the process 3N + 2. 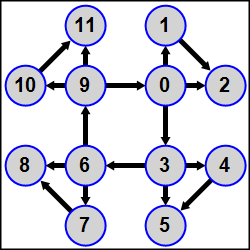
The complete definition of the graph topology should be given in the master process (whereas the second parameter of the MPI_Dist_graph_create function should be equal to 0 in all slave processes). The weights parameter should be equal to MPI_UNWEIGHTED, the info parameter should be equal to MPI_INFO_NULL, ranks of processes should not be reordered. Using the MPI_Send and MPI_Recv functions, send the given numbers from the source processes to the destination processes and output the sum of the given number A and all received numbers in each process. The amount and ranks of source and destination processes should be determined by means of the MPI_Dist_graph_neighbors_count and MPI_Dist_graph_neighbors functions.
MPI5Comm32°. The number of processes is in the range 4 to 15; an integer A is given in each process. Using the MPI_Dist_graph_create function, define a distributed graph topology for all processes as follows: all processes form a binary tree with the process 0 as a tree root, the processes 1 and 2 as a tree nodes of level 1, the processes from 3 to 6 as a tree nodes of level 2 (the processes 3 and 4 are the child nodes of the process 1 and the processes 5 and 6 are the child nodes of the process 2), and so on. Each process is the source for all its child nodes, so each process has 0 to 2 destination processes. 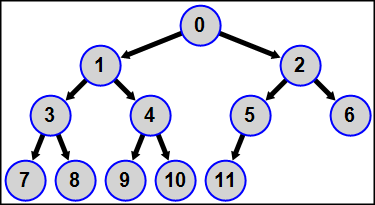
The complete definition of the graph topology should be given in the master process (whereas the second parameter of the MPI_Dist_graph_create function should be equal to 0 in all slave processes). The weights parameter should be equal to MPI_UNWEIGHTED, the info parameter should be equal to MPI_INFO_NULL, ranks of processes should not be reordered. Using the MPI_Send and MPI_Recv functions in each process, find and output the sum of the given number A and all the numbers that are given in ancestors of all levels—from the tree root (the master process) to the nearest ancestor (the parent process). The amount and ranks of source and destination processes should be determined by means of the MPI_Dist_graph_neighbors_count and MPI_Dist_graph_neighbors functions.
Non-blocking collective functions (MPI-3)
MPI5Comm33°. A sequence of 5 real numbers is given in the process of rank K/2, where K is the number of processes. Use the MPI_Ibcast function for an appropriate communicator to send these numbers to processes with lower ranks and output the numbers in processes with ranks from 0 to K/2. Use the MPI_Wait function to check if the MPI_Ibcast non-blocking operation finishes. Additionally, display the duration of each call of MPI_Wait function in milliseconds for processes with ranks from 0 to K/2 in the debug section; for this purpose, call MPI_Wtime before and after MPI_Wait and use the Show function to display the difference of values returned by MPI_Wtime multiplied by 1000.
MPI5Comm34°. A sequence of 5 integers is given in each process of odd rank. Using the MPI_Igather function for an appropriate communicator, send these numbers to a process of rank 1 and output them in descending order of ranks of the processes that sent them (first output the sequence of numbers given in the process with the highest odd rank, last — the sequence of numbers given in the process of rank 1). Use the MPI_Test function to check if the MPI_Igather non-blocking operation finishes; call the MPI_Test function in a loop until it returns a non-zero flag. Additionally, display the number of required loop iterations with MPI_Test calls in the debug section for all odd-rank processes using the Show function.
MPI5Comm35°. A sequence of R + 2 integers is given in each process of even rank, where the number R equals the rank of the process (process 0 has 2 numbers, process 2 has 4 numbers, and so on). Use the MPI_Igatherv function for an appropriate communicator to send these numbers to master process. Output these numbers in ascending order of the ranks of the processes that sent them (first output the sequence of numbers given in the master process). Use MPI_Wait function to check if MPI_Igatherv non-blocking operation finishes. Additionally, display the duration of each call to the MPI_Wait function in milliseconds for even-rank processes in the debug section; for this purpose, call MPI_Wtime before and after MPI_Wait and use the Show function to display the difference of the values returned by MPI_Wtime multiplied by 1000.
MPI5Comm36°. The number of processes K is an even number. A sequence of K/2 real numbers is given in the master process. Use the MPI_Iscatter function for an appropriate communicator to send a number to each process of even rank (including the master process) and output the received number in each process; the numbers must be sent to the processes in reverse order: the first number must be sent to the last process of even rank, the last number — to the process of rank 0. Use the MPI_Test function to check if the MPI_Iscatter non-blocking operation finishes; call the MPI_Test function in a loop until it returns a non-zero flag. Additionally, display the number of required loop iterations with MPI_Test calls in the debug section for all even-rank processes using the Show function.
MPI5Comm37°. The number of processes K is an even number. A sequence of K/2 + 2 real numbers is given in the process of rank 1. Using the MPI_Iscatterv function for an appropriate communicator, send three numbers of given sequence to each process of odd rank, with the first three numbers sent to the process of rank 1, the second, the third and the fourth numbers sent to the process of rank 3, and so on. Output the received numbers in each process. Use the MPI_Wait function to check if the MPI_Iscatterv non-blocking operation finishes. Additionally, display the duration of each call to the MPI_Wait function in milliseconds for odd-rank processes in the debug section; for this purpose, call MPI_Wtime before and after MPI_Wait and use the Show function to display the difference of values returned by MPI_Wtime multiplied by 1000.
MPI5Comm38°. An integer N is given in each process; the number N can take two values: 0 and 1 (there is at least one process with N = 1). Also a real number A is given in each process with N = 1. Use the MPI_Iallgather function to send the number A to each process for which N = 1 and output the numbers in each process in ascending order of the ranks of the processes that sent the numbers (including the number received from the same process). Use the MPI_Test function to check if the MPI_Iallgather non-blocking operation finishes; call the MPI_Test function in a loop until it returns a non-zero flag. Additionally, display the number of required loop iterations with MPI_Test calls in the debug section for all processes with N = 1 using the Show function.
MPI5Comm39°. An integer N is given in each process; the number N can take two values: 0 and 1 (there is at least one process with N = 1). Also, a sequence A of integers is given in each process with N = 1 and it is known that the sequence A in the first process with N = 1 includes one number, the sequence A in the second process with N = 1 includes two numbers, and so on. Use the MPI_Iallgatherv function to send the sequences of numbers A to all processes with N = 1 and output the numbers in each process in ascending order of the ranks of the processes that sent them (including the numbers received from the same process). Use the MPI_Wait function to check if the MPI_Iallgatherv non-blocking operation finishes. Additionally, display the duration of each call of MPI_Wait in milliseconds for all processes with N = 1 in the debug section. For this purpose, call MPI_Wtime before and after MPI_Wait and use the Show function to display the difference of values returned by MPI_Wtime multiplied by 1000.
MPI5Comm40°. A sequence of 2K integers is given in each process of even rank; K is the number of even-rank processes. Using the MPI_Ialltoall function, send two elements of each given sequence to each process of even rank as follows: the initial two elements of each sequence should be sent to the master process, the next two elements of each sequence should be sent to the process of rank 2, and so on. Output received numbers in each even-rank process in ascending order of ranks of sending processes (including the numbers received from the same process). Use the MPI_Test function to check if the MPI_Ialltoall non-blocking operation finishes; call the MPI_Test function in a loop until it returns a non-zero flag. Additionally, display the number of required loop iterations with MPI_Test calls in the debug section for all even-rank processes using the Show function.
MPI5Comm41°. A sequence of K + 1 integers is given in each process of odd rank; K is the number of odd-rank processes. Using the MPI_Ialltoallv function, send two elements of each given sequence to each odd-rank process as follows: the initial two elements of each sequence should be sent to the process 1, the second element and the third element of each sequence should be sent to the process 3, …, the last two elements of each sequence should be sent to the last odd-rank process. Output received numbers in each odd-rank process in ascending order of ranks of sending processes (including the numbers received from the same process). Use MPI_Wait function to check if MPI_Ialltoallv non-blocking operation finishes. Additionally, display the duration of each call to the MPI_Wait function in milliseconds for all odd-rank processes in the debug section; for this purpose, call MPI_Wtime before and after MPI_Wait and use the Show function to display the difference of the values returned by MPI_Wtime multiplied by 1000.
MPI5Comm42°. A sequence of K + 5 real numbers is given in each process of even rank; K is the number of even-rank processes. Find the maximal value among the elements of all given sequences with the same order number using the MPI_Ireduce function with the MPI_MAX operation. Output received maximal values in the master process. Use the MPI_Test function to check if the MPI_Ireduce non-blocking operation finishes; call the MPI_Test function in a loop until it returns a non-zero flag. Additionally, display the number of required loop iterations with MPI_Test calls in the debug section for all even-rank processes using the Show function.
MPI5Comm43°. An integer N is given in each process; the number N can take two values: 0 and 1 (there is at least one process with N = 1). Also a sequence of K real numbers, where K is the number of processes with N = 1, is given in each process with N = 1. Find products of elements of all given sequences with the same order number using the MPI_Iallreduce function with the MPI_PROD operation. Output received products in each process with N = 1. Use the MPI_Wait function to check if the MPI_Iallreduce non-blocking operation finishes. Additionally, display the duration of each call of MPI_Wait in milliseconds for all processes with N = 1 in the debug section. For this purpose, call MPI_Wtime before and after MPI_Wait and use the Show function to display the difference of values returned by MPI_Wtime multiplied by 1000.
MPI5Comm44°. The number of processes is 2K, and it is known that the number K is odd. A sequence of N integers is given in each process with ranks from 0 to K, where N = 3(1 + K)/2. Using the MPI_Ireduce_scatter function, find sums of elements of all given sequences with the same order number and send sums to processes with ranks from 0 to K as follows: the first two sums should be sent to the process 0, the third sum should be sent to the process 1, the fourth and the fifth sum should be sent to the process 2, the sixth sum should be sent to the process 3, and so on (two sums are sent to the even-rank processes and one sum is sent to the odd-rank processes). Output the received sums in each process. Use the MPI_Test function to check if the MPI_Ireduce_scatter non-blocking operation finishes; call the MPI_Test function in a loop until it returns a non-zero flag. Additionally, display the number of required loop iterations with MPI_Test calls in the debug section for processes with ranks from 0 to K using the Show function.
MPI5Comm45°. A sequence of 3K integers is given in each process of even rank; K is the number of even-rank processes. Using the MPI_Ireduce_scatter_block function, find sums of elements of all given sequences with the same order number and send three sums to each even-rank process as follows: the first three sums should be sent to the process 0, the next three sums should be sent to the process 2, and so on. Output the received sums in each process. Use the MPI_Wait function to check if the MPI_Ireduce_scatter_block non-blocking operation finishes. Additionally, display the duration of each call of MPI_Wait in milliseconds for all even-rank processes in the debug section. For this purpose, call MPI_Wtime before and after MPI_Wait and use the Show function to display the difference of values returned by MPI_Wtime multiplied by 1000. Note. The corresponding blocking collective function MPI_Reduce_scatter_block appeared in the MPI-2 standard. It simplifies the distribution of reduction results to different processes (compared to the MPI_Reduce_scatter function) if each process must receive a reduction dataset of the same size.
MPI5Comm46°. A sequence of K + 5 integers is given in each even-rank process; 2K is the number of processes. Using the MPI_Iscan function, find maximal values among elements of given sequences with the same order number as follows: the maximal values of elements of sequences given in the processes of even ranks 0, 2, …, R should be found in the process R (R = 0, 2, …, 2K − 2). Output received data in each process. Use the MPI_Test function to check if the MPI_Iscan non-blocking operation finishes; call the MPI_Test function in a loop until it returns a non-zero flag. Additionally, display the number of required loop iterations with MPI_Test calls in the debug section for even-rank processes using the Show function.
MPI5Comm47°. A sequence of K + 5 integers is given in each odd-rank process; 2K is the number of processes. Using the MPI_Iexscan function, find minimal values among elements of given sequences with the same order number as follows: the minimal values of elements of sequences given in the processes of odd ranks 1, 3, …, R − 2 should be found in the process of rank R, R = 3, 5, …, 2K − 1). Output received data in processes of rank R. Use MPI_Wait function to check if MPI_Iexscan non-blocking operation finishes. Additionally, display the duration of each call to the MPI_Wait function in milliseconds for even-rank processes in the debug section; for this purpose, call MPI_Wtime before and after MPI_Wait and use the Show function to display the difference of the values returned by MPI_Wtime multiplied by 1000. Note. The corresponding blocking collective function MPI_Exscan ("exclusive scan") appeared in the MPI-2 standard. It is more general than the MPI_Scan function, because it allows to model the MPI_Scan function ("inclusive scan") without performing additional collective operations (it is enough, after applying the MPI_Exscan function, to call the local function MPI_Reduce_local, which also appeared in the MPI-2 standard). It should be noted that the inverse action (modeling the MPI_Exscan function with the MPI_Scan function) is not possible for some reduction operations (in particular, such action is not possible for the operations of finding the minimum or maximum).
|






