|
|
Группы процессов и коммуникаторы
Создание новых коммуникаторов
MPI5Comm1°. В главном процессе дан набор из K целых чисел, где K — количество процессов четного ранга (0, 2, …). С помощью функций MPI_Comm_group, MPI_Group_incl и MPI_Comm_create создать новый коммуникатор, включающий процессы четного ранга. Используя одну коллективную операцию пересылки данных для созданного коммуникатора, переслать по одному исходному числу в каждый процесс четного ранга (включая главный) и вывести полученные числа.
MPI5Comm2°. В каждом процессе нечетного ранга (1, 3, …) даны два вещественных числа. С помощью функций MPI_Comm_group, MPI_Group_excl и MPI_Comm_create создать новый коммуникатор, включающий процессы нечетного ранга. Используя одну коллективную операцию пересылки данных для созданного коммуникатора, переслать исходные числа во все процессы нечетного ранга и вывести эти числа в порядке возрастания рангов переславших их процессов (включая числа, полученные из этого же процесса).
MPI5Comm3°. В каждом процессе, ранг которого делится на 3 (включая главный процесс), даны три целых числа. С помощью функции MPI_Comm_split создать новый коммуникатор, включающий процессы, ранг которых делится на 3. Используя одну коллективную операцию пересылки данных для созданного коммуникатора, переслать исходные числа в главный процесс и вывести эти числа в порядке возрастания рангов переславших их процессов (включая числа, полученные из главного процесса). Указание. При вызове функции MPI_Comm_split в процессах, которые не требуется включать в новый коммуникатор, в качестве параметра color следует указывать константу MPI_UNDEFINED.
MPI5Comm4°. В каждом процессе четного ранга (включая главный процесс) дан набор из трех элементов — вещественных чисел. Используя новый коммуникатор и одну коллективную операцию редукции, найти минимальные значения среди элементов исходных наборов с одним и тем же порядковым номером и вывести найденные минимумы в главном процессе. Новый коммуникатор создать с помощью функции MPI_Comm_split. Указание. См. указание к задаче MPI5Comm3.
MPI5Comm5°. В каждом процессе дано вещественное число. Используя функцию MPI_Comm_split и одну коллективную операцию редукции, найти максимальное из чисел, данных в процессах с четным рангом (включая главный процесс), и минимальное из чисел, данных в процессах с нечетным рангом. Найденный максимум вывести в процессе 0, а найденный минимум — в процессе 1. Указание. Программа должна содержать единственный вызов функции MPI_Comm_split, создающий оба требуемых коммуникатора (каждый в соответствующей группе процессов).
MPI5Comm6°. В главном процессе дано целое число K и набор из K вещественных чисел, в каждом подчиненном процессе дано целое число N, которое может принимать два значения: 0 и 1 (количество подчиненных процессов с N = 1 равно K). Используя функцию MPI_Comm_split и одну коллективную операцию пересылки данных, переслать по одному вещественному числу из главного процесса в каждый подчиненный процесс с N = 1 и вывести в этих подчиненных процессах полученные числа. Указание. См. указание к задаче MPI5Comm3.
MPI5Comm7°. В каждом процессе дано целое число N, которое может принимать два значения: 0 и 1 (имеется хотя бы один процесс с N = 1). Кроме того, в каждом процессе с N = 1 дано вещественное число A. Используя функцию MPI_Comm_split и одну коллективную операцию пересылки данных, переслать числа A в первый из процессов с N = 1 и вывести их в порядке возрастания рангов переславших их процессов (включая число, полученное из этого же процесса). Указание. См. указание к задаче MPI5Comm3.
MPI5Comm8°. В каждом процессе дано целое число N, которое может принимать два значения: 0 и 1 (имеется хотя бы один процесс с N = 1). Кроме того, в каждом процессе с N = 1 дано вещественное число A. Используя функцию MPI_Comm_split и одну коллективную операцию пересылки данных, переслать числа A в последний из процессов с N = 1 и вывести их в порядке возрастания рангов переславших их процессов (включая число, полученное из этого же процесса). Указание. См. указание к задаче MPI5Comm3.
MPI5Comm9°. В каждом процессе дано целое число N, которое может принимать два значения: 0 и 1 (имеется хотя бы один процесс с N = 1). Кроме того, в каждом процессе с N = 1 дано вещественное число A. Используя функцию MPI_Comm_split и одну коллективную операцию пересылки данных, переслать числа A во все процессы с N = 1 и вывести их в порядке возрастания рангов переславших их процессов (включая число, полученное из этого же процесса). Указание. См. указание к задаче MPI5Comm3.
MPI5Comm10°. В каждом процессе дано целое число N, которое может принимать два значения: 1 и 2 (имеется хотя бы один процесс с каждым из возможных значений). Кроме того, в каждом процессе дано целое число A. Используя функцию MPI_Comm_split и одну коллективную операцию пересылки данных, переслать числа A, данные в процессах с N = 1, во все процессы с N = 1, а числа A, данные в процессах с N = 2, во все процессы с N = 2. Во всех процессах вывести полученные числа в порядке возрастания рангов переславших их процессов (включая число, полученное из этого же процесса). Указание. См. указание к задаче MPI5Comm5.
MPI5Comm11°. В каждом процессе дано целое число N, которое может принимать два значения: 0 и 1 (имеется хотя бы один процесс с N = 1). Кроме того, в каждом процессе с N = 1 дано вещественное число A. Используя функцию MPI_Comm_split и одну коллективную операцию редукции, найти сумму всех исходных чисел A и вывести ее во всех процессах с N = 1. Указание. См. указание к задаче MPI5Comm3.
MPI5Comm12°. В каждом процессе дано целое число N, которое может принимать два значения: 1 и 2 (имеется хотя бы один процесс с каждым из возможных значений). Кроме того, в каждом процессе дано вещественное число A. Используя функцию MPI_Comm_split и одну коллективную операцию редукции, найти минимальное значение среди чисел A, которые даны в процессах с N = 1, и максимальное значение среди чисел A, которые даны в процессах с N = 2. Найденный минимум вывести в процессах с N = 1, а найденный максимум — в процессах с N = 2. Указание. См. указание к задаче MPI5Comm5.
Виртуальные топологии
MPI5Comm13°. В главном процессе дано целое число N (> 1), причем известно, что количество процессов K делится на N. Переслать число N во все процессы, после чего, используя функцию MPI_Cart_create, определить для всех процессов декартову топологию в виде двумерной решетки — матрицы размера N × K/N (порядок нумерации процессов оставить прежним). Используя функцию MPI_Cart_coords, вывести для каждого процесса его координаты в созданной топологии.
MPI5Comm14°. В главном процессе дано целое число N (> 1), не превосходящее количества процессов K. Переслать число N во все процессы, после чего определить декартову топологию для начальной части процессов в виде двумерной решетки — матрицы размера N × K/N (символ «/» обозначает операцию деления нацело, порядок нумерации процессов следует оставить прежним). Для каждого процесса, включенного в декартову топологию, вывести его координаты в этой топологии.
MPI5Comm15°. Число процессов К является четным: K = 2N, N > 1. В процессах 0 и N дано по одному вещественному числу A. Определить для всех процессов декартову топологию в виде матрицы размера 2 × N, после чего, используя функцию MPI_Cart_sub, расщепить матрицу процессов на две одномерные строки (при этом процессы 0 и N будут главными процессами в полученных строках). Используя одну коллективную операцию пересылки данных, переслать число A из главного процесса каждой строки во все процессы этой же строки и вывести полученное число в каждом процессе (включая процессы 0 и N).
MPI5Comm16°. Число процессов К является четным: K = 2N, N > 1. В процессах 0 и 1 дано по одному вещественному числу A. Определить для всех процессов декартову топологию в виде матрицы размера N × 2, после чего, используя функцию MPI_Cart_sub, расщепить матрицу процессов на два одномерных столбца (при этом процессы 0 и 1 будут главными процессами в полученных столбцах). Используя одну коллективную операцию пересылки данных, переслать число A из главного процесса каждого столбца во все процессы этого же столбца и вывести полученное число в каждом процессе (включая процессы 0 и 1).
MPI5Comm17°. Число процессов К кратно трем: K = 3N, N > 1. В процессах 0, N и 2N дано по N целых чисел. Определить для всех процессов декартову топологию в виде матрицы размера 3 × N, после чего, используя функцию MPI_Cart_sub, расщепить матрицу процессов на три одномерные строки (при этом процессы 0, N и 2N будут главными процессами в полученных строках). Используя одну коллективную операцию пересылки данных, переслать по одному исходному числу из главного процесса каждой строки во все процессы этой же строки и вывести полученное число в каждом процессе (включая процессы 0, N и 2N).
MPI5Comm18°. Число процессов К кратно трем: K = 3N, N > 1. В процессах 0, 1 и 2 дано по N целых чисел. Определить для всех процессов декартову топологию в виде матрицы размера N × 3, после чего, используя функцию MPI_Cart_sub, расщепить матрицу процессов на три одномерных столбца (при этом процессы 0, 1 и 2 будут главными процессами в полученных столбцах). Используя одну коллективную операцию пересылки данных, переслать по одному исходному числу из главного процесса каждого столбца во все процессы этого же столбца и вывести полученное число в каждом процессе (включая процессы 0, 1 и 2).
MPI5Comm19°. Количество процессов K равно 8 или 12, в каждом процессе дано целое число. Определить для всех процессов декартову топологию в виде трехмерной решетки размера 2 × 2 × K/4 (порядок нумерации процессов оставить прежним). Интерпретируя эту решетку как две матрицы размера 2 × K/4 (в одну матрицу входят процессы с одинаковой первой координатой), расщепить каждую матрицу процессов на две одномерные строки. Используя одну коллективную операцию пересылки данных, переслать в главный процесс каждой строки исходные числа из процессов этой же строки и вывести полученные наборы чисел (включая числа, полученные из главных процессов строк).
MPI5Comm20°. Количество процессов K равно 8 или 12, в каждом процессе дано целое число. Определить для всех процессов декартову топологию в виде трехмерной решетки размера 2 × 2 × K/4 (порядок нумерации процессов оставить прежним). Интерпретируя полученную решетку как K/4 матриц размера 2 × 2 (в одну матрицу входят процессы с одинаковой третьей координатой), расщепить эту решетку на K/4 указанных матриц. Используя одну коллективную операцию пересылки данных, переслать в главный процесс каждой из полученных матриц исходные числа из процессов этой же матрицы и вывести полученные наборы чисел (включая числа, полученные из главных процессов матриц).
MPI5Comm21°. Количество процессов K равно 8 или 12, в каждом процессе дано вещественное число. Определить для всех процессов декартову топологию в виде трехмерной решетки размера 2 × 2 × K/4 (порядок нумерации процессов оставить прежним). Интерпретируя эту решетку как две матрицы размера 2 × K/4 (в одну матрицу входят процессы с одинаковой первой координатой), расщепить каждую матрицу процессов на K/4 одномерных столбцов. Используя одну коллективную операцию редукции, для каждого столбца процессов найти произведение исходных чисел и вывести найденные произведения в главных процессах каждого столбца.
MPI5Comm22°. Количество процессов K равно 8 или 12, в каждом процессе дано вещественное число. Определить для всех процессов декартову топологию в виде трехмерной решетки размера 2 × 2 × K/4 (порядок нумерации процессов оставить прежним). Интерпретируя полученную решетку как K/4 матриц размера 2 × 2 (в одну матрицу входят процессы с одинаковой третьей координатой), расщепить эту решетку на K/4 указанных матриц. Используя одну коллективную операцию редукции, для каждой из полученных матриц найти сумму исходных чисел и вывести найденные суммы в каждом процессе соответствующей матрицы.
MPI5Comm23°. В главном процессе даны положительные целые числа M и N, произведение которых не превосходит количества процессов; кроме того, в процессах с рангами от 0 до M·N − 1 даны целые числа X и Y. Переслать числа M и N во все процессы, после чего определить для начальных M·N процессов декартову топологию в виде двумерной решетки размера M × N, являющейся периодической по первому измерению (порядок нумерации процессов оставить прежним). В каждом процессе, входящем в созданную топологию, вывести ранг процесса с координатами X, Y (с учетом периодичности), используя для этого функцию MPI_Cart_rank. В случае недопустимых координат вывести −1. Примечание. Если при вызове функции MPI_Cart_rank указаны недопустимые координаты (например, отрицательные координаты для измерений, по которым декартова решетка не является периодической), то сама функция возвращает ненулевое значение (являющееся признаком ошибки), а возвращаемое значение параметра rank является неопределенным. Таким образом, в данном задании число −1 следует выводить, если функция MPI_Cart_rank вернула ненулевое значение. Чтобы подавить возникающие при этом сообщения об ошибках, отображаемые в разделе отладки окна задачника, достаточно перед вызовом функции, который может привести к ошибке, установить с помощью функции MPI_Comm_set_errhandler (MPI_Errhandler_set в MPI-1) специальный вариант обработчика ошибок MPI_ERRORS_RETURN, который при возникновении ошибки не выполняет никаких действий, кроме установки ненулевого возвращаемого значения для этой функции. Следует заметить, что в версии MPICH 1.2.5 в случае указания недопустимых координат функция MPI_Cart_rank возвращает значение параметра rank, равное −1, что позволяет упростить решение, избавившись от проверки возвращаемого значения функции. Однако и в этом случае желательно подавить вывод сообщений об ошибках описанным выше способом.
MPI5Comm24°. В главном процессе даны положительные целые числа M и N, произведение которых не превосходит количества процессов; кроме того, в процессах с рангами от 0 до M·N − 1 даны целые числа X и Y. Переслать числа M и N во все процессы, после чего определить для начальных M·N процессов декартову топологию в виде двумерной решетки размера M × N, являющейся периодической по второму измерению (порядок нумерации процессов оставить прежним). В каждом процессе, входящем в созданную топологию, вывести ранг процесса с координатами X, Y (с учетом периодичности), используя для этого функцию MPI_Cart_rank. В случае недопустимых координат вывести −1. Примечание. См. примечание к заданию MPI5Comm23.
MPI5Comm25°. В каждом подчиненном процессе дано вещественное число. Определить для всех процессов декартову топологию в виде одномерной решетки и осуществить простой сдвиг исходных данных с шагом −1 (число из каждого подчиненного процесса пересылается в предыдущий процесс). Для определения рангов посылающих и принимающих процессов использовать функцию MPI_Cart_shift, пересылку выполнять с помощью функций MPI_Send и MPI_Recv. Во всех процессах, получивших данные, вывести эти данные.
MPI5Comm26°. Число процессов К является четным: K = 2N, N > 1; в каждом процессе дано вещественное число A. Определить для всех процессов декартову топологию в виде матрицы размера 2 × N (порядок нумерации процессов оставить прежним) и для каждой строки матрицы осуществить циклический сдвиг исходных данных с шагом 1 (число A из каждого процесса, кроме последнего в строке, пересылается в следующий процесс этой же строки, а из последнего процесса — в главный процесс этой строки). Для определения рангов посылающих и принимающих процессов использовать функцию MPI_Cart_shift, пересылку выполнять с помощью функции MPI_Sendrecv. Во всех процессах вывести полученные данные.
MPI5Comm27°. Количество процессов K равно 8 или 12, в каждом процессе дано вещественное число. Определить для всех процессов декартову топологию в виде трехмерной решетки размера 2 × 2 × K/4 (порядок нумерации процессов оставить прежним). Интерпретируя полученную решетку как K/4 матриц размера 2 × 2 (в одну матрицу входят процессы с одинаковой третьей координатой, матрицы упорядочены по возрастанию третьей координаты), осуществить циклический сдвиг исходных данных из процессов каждой матрицы в соответствующие процессы следующей матрицы (из процессов последней матрицы данные перемещаются в первую матрицу). Для определения рангов посылающих и принимающих процессов использовать функцию MPI_Cart_shift, пересылку выполнять с помощью функции MPI_Sendrecv_replace. Во всех процессах вывести полученные данные.
MPI5Comm28°. Число процессов K является нечетным: K = 2N + 1 (1 < N < 5); в каждом процессе дано целое число A. Используя функцию MPI_Graph_create, определить для всех процессов топологию графа, в которой главный процесс связан ребрами со всеми процессами нечетного ранга (1, 3, …, 2N − 1), а каждый процесс четного положительного ранга R (2, 4, …, 2N) связан ребром с процессом ранга R − 1 (в результате получается N-лучевая звезда, центром которой является главный процесс, а каждый луч состоит из двух подчиненных процессов R и R + 1, причем ближайшим к центру является процесс нечетного ранга R). 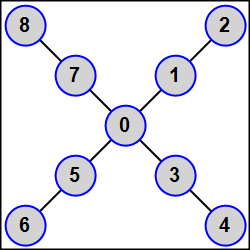
Переслать число A из каждого процесса всем процессам, связанным с ним ребрами (процессам-соседям). Для определения количества процессов-соседей и их рангов использовать функции MPI_Graph_neighbors_count и MPI_Graph_neighbors, пересылку выполнять с помощью функций MPI_Send и MPI_Recv. Во всех процессах вывести полученные числа в порядке возрастания рангов переславших их процессов.
MPI5Comm29°. Число процессов K является четным: K = 2N (1 < N < 6); в каждом процессе дано целое число A. Используя функцию MPI_Graph_create, определить для всех процессов топологию графа, в которой все процессы четного ранга (включая главный процесс) связаны в цепочку: 0 — 2 — 4 — 6 — … — (2N − 2), а каждый процесс нечетного ранга R (1, 3, …, 2N − 1) связан с процессом ранга R − 1 (в результате каждый процесс нечетного ранга будет иметь единственного соседа, первый и последний процессы четного ранга будут иметь по два соседа, а остальные — «внутренние» — процессы четного ранга будут иметь по три соседа). 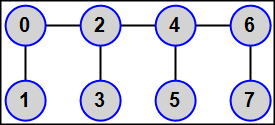
Переслать число A из каждого процесса всем процессам-соседям. Для определения количества процессов-соседей и их рангов использовать функции MPI_Graph_neighbors_count и MPI_Graph_neighbors, пересылку выполнять с помощью функции MPI_Sendrecv. Во всех процессах вывести полученные числа в порядке возрастания рангов переславших их процессов.
MPI5Comm30°. Количество процессов K равно 3N + 1 (1 < N < 5); в каждом процессе дано целое число A. Используя функцию MPI_Graph_create, определить для всех процессов топологию графа, в которой процессы R, R + 1, R + 2, где R = 1, 4, 7, …, связаны между собой ребрами, и, кроме того, каждый процесс положительного ранга, кратного трем (3, 6, …), связан ребром с главным процессом (в результате получается N-лучевая звезда, центром которой является главный процесс, а каждый луч состоит из трех связанных между собой процессов, причем с центром связан процесс ранга, кратного трем). 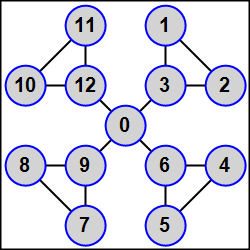
Переслать число A из каждого процесса всем процессам-соседям. Для определения количества процессов-соседей и их рангов использовать функции MPI_Graph_neighbors_count и MPI_Graph_neighbors, пересылку выполнять с помощью функции MPI_Sendrecv. Во всех процессах вывести полученные числа в порядке возрастания рангов переславших их процессов.
Топология распределенного графа (MPI-2)
MPI5Comm31°. Количество процессов K кратно 3; в каждом процессе дано целое число A. Используя функцию MPI_Dist_graph_create, определить для всех процессов топологию распределенного графа, в которой все процессы рангов, кратных 3 (0, 3, …, K − 3) образуют кольцо, причем каждый из процессов, входящих в кольцо, является источником для последующего процесса (процесс 0 является источником для процесса 3, процесс 3 — для процесса 6, …, процесс K − 3 — для процесса 0) и, кроме того, процесс ранга 3N (N = 0, 1, …, K/3 − 1) является источником для процессов ранга 3N + 1 и 3N + 2, а процесс ранга 3N + 1 является источником для процесса ранга 3N + 2. 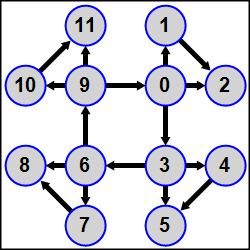
Полное определение топологии дать в главном процессе (в подчиненных процессах второй параметр функции MPI_Dist_graph_create должен быть равен 0); параметр weights положить равным MPI_UNWEIGHTED, параметр info — равным MPI_INFO_NULL, порядок нумерации процессов не изменять. Переслать числа A от процессов-источников процессам-приемникам и вывести в каждом процессе сумму исходного числа A и всех чисел, полученных от процессов-источников. Для определения количества источников и приемников, а также их рангов использовать функции MPI_Dist_graph_neighbors_count и MPI_Dist_graph_neighbors, пересылку выполнять с помощью функций MPI_Send и MPI_Recv.
MPI5Comm32°. Количество процессов лежит в диапазоне от 4 до 15, в каждом процессе дано целое число A. Используя функцию MPI_Dist_graph_create, определить для всех процессов топологию распределенного графа, которая представляет собой бинарное дерево с корнем в главном процессе 0, вершинами первого уровня в процессах рангов 1 и 2, вершинами второго уровня в процессах рангов 3-6 (причем процессы ранга 3 и 4 являются дочерними вершинами процесса 1, а процессы ранга 5 и 6 — дочерними вершинами процесса 2), и т. д. Каждый процесс является источником для своих дочерних вершин; таким образом, каждый процесс имеет от 0 до 2 процессов-приемников. 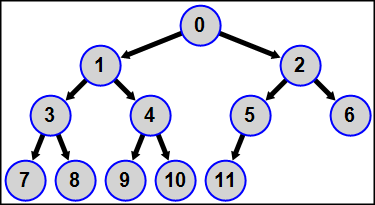
Полное определение топологии дать в главном процессе (в подчиненных процессах второй параметр функции MPI_Dist_graph_create должен быть равен 0); параметр weights положить равным MPI_UNWEIGHTED, параметр info — равным MPI_INFO_NULL, порядок нумерации процессов не изменять. Найти и вывести в каждом процессе сумму исходного числа A и чисел, данных в процессах-предках всех уровней — от корня (главного процесса) до ближайшего предка (родительского процесса-источника). Для определения количества источников и приемников, а также их рангов использовать функции MPI_Dist_graph_neighbors_count и MPI_Dist_graph_neighbors, пересылку данных выполнять с помощью функций MPI_Send и MPI_Recv.
Неблокирующие коллективные функции (MPI-3)
MPI5Comm33°. В процессе ранга K/2 дано 5 чисел; K — количество процессов. Используя функцию MPI_Ibcast для подходящего коммуникатора, переслать эти числа в процессы с меньшими рангами и вывести полученные числа в процессах с рангами от 0 до K/2. Для проверки окончания неблокирующей операции MPI_Ibcast использовать функцию MPI_Wait. Дополнительно для процессов с рангами от 0 до K/2 отобразить в разделе отладки продолжительность каждого вызова функции MPI_Wait в миллисекундах; для этого вызвать функцию MPI_Wtime до и после MPI_Wait и с помощью функции Show вывести разность возвращенных функцией MPI_Wtime значений, умноженную на 1000.
MPI5Comm34°. В каждом процессе нечетного ранга дан набор из 5 целых чисел. Используя функцию MPI_Igather для подходящего коммуникатора, переслать эти числа в процесс ранга 1 и вывести их в порядке убывания рангов переславших их процессов (первым вывести набор чисел, данный в процессе максимального нечетного ранга, последним — набор чисел, данный в процессе ранга 1). Для проверки окончания неблокирующей операции MPI_Igather использовать функцию MPI_Test; вызов функции MPI_Test повторять в цикле до тех пор, пока она не вернет ненулевой флаг. Дополнительно для всех процессов нечетного ранга отобразить в разделе отладки потребовавшееся количество итераций цикла с вызовами MPI_Test, используя функцию Show.
MPI5Comm35°. В каждом процессе четного ранга дан набор из R + 2 целых чисел, где число R равно рангу процесса (в процессе 0 даны 2 числа, в процессе 2 даны 4 числа, и т. д.). Используя функцию MPI_Igatherv для подходящего коммуникатора, переслать эти наборы в главный процесс и вывести полученные наборы в порядке возрастания рангов переславших их процессов (первым вывести набор, данный в главном процессе). Для проверки окончания неблокирующей операции MPI_Igatherv использовать функцию MPI_Wait. Дополнительно для процессов четного ранга отобразить в разделе отладки продолжительность каждого вызова функции MPI_Wait в миллисекундах; для этого вызвать функцию MPI_Wtime до и после MPI_Wait и с помощью функции Show вывести разность возвращенных функцией MPI_Wtime значений, умноженную на 1000.
MPI5Comm36°. Количество процессов K является четным. В главном процессе дан набор из K/2 чисел. Используя функцию MPI_Iscatter для подходящего коммуникатора, переслать по одному числу в каждый процесс четного ранга (включая главный) и вывести в каждом процессе полученное число; при этом числа надо пересылать в процессы в обратном порядке: первое число должно быть послано в последний процесс четного ранга, а последнее число — в процесс ранга 0. Для проверки окончания неблокирующей операции MPI_Iscatter использовать функцию MPI_Test; вызов функции MPI_Test повторять в цикле до тех пор, пока она не вернет ненулевой флаг. Дополнительно для всех процессов четного ранга отобразить в разделе отладки потребовавшееся количество итераций цикла с вызовами MPI_Test, используя функцию Show.
MPI5Comm37°. Количество процессов K является четным. В процессе ранга 1 дан набор из K/2 + 2 чисел. Используя функцию MPI_Iscatterv для подходящего коммуникатора, переслать в каждый процесс нечетного ранга три числа из данного набора, при этом в процесс ранга 1 должны быть пересланы первые три числа, в процесс ранга 3 — числа со второго по четвертое, и т. д. В каждом процессе вывести полученные числа. Для проверки окончания неблокирующей операции MPI_Iscatterv использовать функцию MPI_Wait. Дополнительно для процессов нечетного ранга отобразить в разделе отладки продолжительность каждого вызова функции MPI_Wait в миллисекундах; для этого вызвать функцию MPI_Wtime до и после MPI_Wait и с помощью функции Show вывести разность возвращенных функцией MPI_Wtime значений, умноженную на 1000.
MPI5Comm38°. В каждом процессе дано целое число N, которое может принимать два значения: 0 и 1 (имеется хотя бы один процесс с N = 1). Кроме того, в каждом процессе с N = 1 дано вещественное число A. Используя функцию MPI_Iallgather, переслать числа A во все процессы, для которых N = 1, и вывести их в каждом процессе в порядке возрастания рангов переславших их процессов (включая число, полученное из этого же процесса). Для проверки окончания неблокирующей операции MPI_Iallgather использовать функцию MPI_Test; вызов функции MPI_Test повторять в цикле до тех пор, пока она не вернет ненулевой флаг. Дополнительно для всех процессов с N = 1 отобразить в разделе отладки потребовавшееся количество итераций цикла с вызовами MPI_Test, используя функцию Show.
MPI5Comm39°. В каждом процессе дано целое число N, которое может принимать два значения: 0 и 1 (имеется хотя бы один процесс с N = 1). Кроме того, в каждом процессе с N = 1 дан набор A целых чисел, причем известно, что для первого процесса с N = 1 набор A содержит одно число, для второго процесса с N = 1 набор A содержит два числа, и т. д. Используя функцию MPI_Iallgatherv, переслать наборы чисел A во все процессы, для которых N = 1, и вывести их в каждом процессе в порядке возрастания рангов переславших их процессов (включая числа, полученные из этого же процесса). Для проверки окончания неблокирующей операции MPI_Iallgatherv использовать функцию MPI_Wait. Дополнительно для всех процессов с N = 1 отобразить в разделе отладки продолжительность каждого вызова функции MPI_Wait в миллисекундах; для этого вызвать функцию MPI_Wtime до и после MPI_Wait и с помощью функции Show вывести разность возвращенных функцией MPI_Wtime значений, умноженную на 1000.
MPI5Comm40°. В каждом процессе четного ранга дан набор из 2K целых чисел, где K — количество процессов четного ранга. Используя функцию MPI_Ialltoall, переслать в каждый процесс четного ранга два очередных числа из каждого набора (в главный процесс — первые два числа из каждого набора, в процесс ранга 2 — следующие два числа, и т. д.). В каждом процессе четного ранга вывести числа в порядке возрастания рангов переславших их процессов (включая числа, полученные из этого же процесса). Для проверки окончания неблокирующей операции MPI_Ialltoall использовать функцию MPI_Test; вызов функции MPI_Test повторять в цикле до тех пор, пока она не вернет ненулевой флаг. Дополнительно для всех процессов четного ранга отобразить в разделе отладки потребовавшееся количество итераций цикла с вызовами MPI_Test, используя функцию Show.
MPI5Comm41°. В каждом процессе нечетного ранга дан набор из K + 1 целых чисел, где K — количество процессов нечетного ранга. Используя функцию MPI_Ialltoallv, переслать в каждый процесс нечетного ранга два числа из каждого набора; при этом в процесс 1 надо переслать первые два числа, в процесс 3 — второе и третье число, …, в последний процесс нечетного ранга — последние два числа каждого набора. В каждом процессе нечетного ранга вывести полученные числа в порядке возрастания рангов переславших их процессов (включая числа, полученные из этого же процесса). Для проверки окончания неблокирующей операции MPI_Ialltoallv использовать функцию MPI_Wait. Для всех процессов нечетного ранга отобразить в разделе отладки продолжительность каждого вызова функции MPI_Wait в миллисекундах; для этого вызвать функцию MPI_Wtime до и после MPI_Wait и с помощью функции Show вывести разность возвращенных функцией MPI_Wtime значений, умноженную на 1000.
MPI5Comm42°. В каждом процессе четного ранга дан набор из K + 5 чисел, где K — количество процессов четного ранга. Используя функцию MPI_Ireduce для операции MPI_MAX, найти максимальное значение среди элементов данных наборов с одним и тем же порядковым номером и вывести полученные максимумы в главном процессе. Для проверки окончания неблокирующей операции MPI_Ireduce использовать функцию MPI_Test; вызов функции MPI_Test повторять в цикле до тех пор, пока она не вернет ненулевой флаг. Дополнительно для всех процессов четного ранга отобразить в разделе отладки потребовавшееся количество итераций цикла с вызовами MPI_Test, используя функцию Show.
MPI5Comm43°. В каждом процессе дано целое число N, которое может принимать два значения: 0 и 1 (имеется хотя бы один процесс с N = 1). Кроме того, в каждом процессе с N = 1 дан набор из K чисел, где K = количество процессов с N = 1. Используя функцию MPI_Iallreduce для операции MPI_PROD, перемножить элементы данных наборов с одним и тем же порядковым номером и вывести полученные произведения во всех процессах с N = 1. Для проверки окончания неблокирующей операции MPI_Iallreduce использовать функцию MPI_Wait. Дополнительно для всех процессов с N = 1 отобразить в разделе отладки продолжительность каждого вызова функции MPI_Wait в миллисекундах; для этого вызвать функцию MPI_Wtime до и после MPI_Wait и с помощью функции Show вывести разность возвращенных функцией MPI_Wtime значений, умноженную на 1000.
MPI5Comm44°. Количество процессов равно 2K, причем известно, что число K является нечетным. В каждом процессе ранга от 0 до K дан набор из N целых чисел, где N = 3(1 + K)/2. Используя функцию MPI_Ireduce_scatter, просуммировать элементы данных наборов с одним и тем же порядковым номером и переслать полученные суммы в процессы ранга от 0 до K следующим образом: первые две суммы — в процесс 0, третью сумму — в процесс 1, четвертую и пятую сумму — в процесс 2, шестую сумму — в процесс 3, и т. д. (в процессы четного ранга пересылаются по две очередные суммы, а в процессы нечетного ранга — по одной). Вывести в каждом процессе полученные суммы. Для проверки окончания неблокирующей операции MPI_Ireduce_scatter использовать функцию MPI_Test; вызов функции MPI_Test повторять в цикле до тех пор, пока она не вернет ненулевой флаг. Дополнительно для всех процессов с рангами от 0 до K отобразить в разделе отладки потребовавшееся количество итераций цикла с вызовами MPI_Test, используя функцию Show.
MPI5Comm45°. В каждом процессе четного ранга дан набор из 3K целых чисел, где K — количество процессов четного ранга. Используя функцию MPI_Ireduce_scatter_block, просуммировать элементы данных наборов с одним и тем же порядковым номером, переслать по три полученных суммы в каждый процесс четного ранга (первые три суммы — в процесс 0, следующие три суммы — в процесс 2, и т. д.) и вывести в каждом процессе полученные суммы. Для проверки окончания неблокирующей операции MPI_Ireduce_scatter_block использовать функцию MPI_Wait. Дополнительно для всех процессов с четными рангами отобразить в разделе отладки продолжительность каждого вызова функции MPI_Wait в миллисекундах; для этого вызвать функцию MPI_Wtime до и после MPI_Wait и с помощью функции Show вывести разность возвращенных функцией MPI_Wtime значений, умноженную на 1000. Примечание. Соответствующая блокирующая коллективная функция MPI_Reduce_scatter_block появилась в стандарте MPI-2. Она упрощает раcпределение результатов редукции по различным процессам (по сравнению с функцией MPI_Reduce_scatter), если в каждый процесс требуется передать набор данных одного и того же размера.
MPI5Comm46°. В каждом процессе четного ранга дан набор из K + 5 целых чисел, где 2K — количество процессов. Используя функцию MPI_Iscan, найти в процессе четного ранга R (R = 0, 2, …, 2K − 2) максимальные значения среди элементов с одним и тем же порядковым номером для наборов, данных в процессах с рангами 0, 2, …, R, и вывести в каждом процессе найденные максимумы. Для проверки окончания неблокирующей операции MPI_Iscan использовать функцию MPI_Test; вызов функции MPI_Test повторять в цикле до тех пор, пока она не вернет ненулевой флаг. Дополнительно для всех процессов с четными рангами отобразить в разделе отладки потребовавшееся количество итераций цикла с вызовами MPI_Test, используя функцию Show.
MPI5Comm47°. В каждом процессе нечетного ранга дан набор из K + 5 целых чисел, где 2K — количество процессов. Используя функцию MPI_Iexscan, найти в процессах нечетного ранга R, начиная с ранга 3 (R = 3, 5, …, 2K − 1), минимальные значения среди элементов с одним и тем же порядковым номером для наборов, данных в процессах с нечетными рангами 1, 3, …, R − 2, и вывести в процессах ранга R найденные минимумы. Для проверки окончания неблокирующей операции MPI_Iexscan использовать функцию MPI_Wait. Дополнительно для процессов нечетного ранга отобразить в разделе отладки продолжительность каждого вызова функции MPI_Wait в миллисекундах; для этого вызвать функцию MPI_Wtime до и после MPI_Wait и с помощью функции Show вывести разность возвращенных функцией MPI_Wtime значений, умноженную на 1000. Примечание. Соответствующая блокирующая коллективная функция MPI_Exscan («exclusive scan») появилась в стандарте MPI-2. Она является более универсальной, чем функция MPI_Scan, так как позволяет промоделировать функцию MPI_Scan («inclusive scan») без выполнения дополнительных коллективных операций (достаточно после применения функции MPI_Exscan вызвать локальную функцию MPI_Reduce_local, которая также появилась в стандарте MPI-2). Следует заметить, что обратное действие (моделирование функции MPI_Exscan с помощью функции MPI_Scan) возможно не для всех операций редукции (в частности, такое действие невозможно для операций нахождения минимума или максимума).
|






