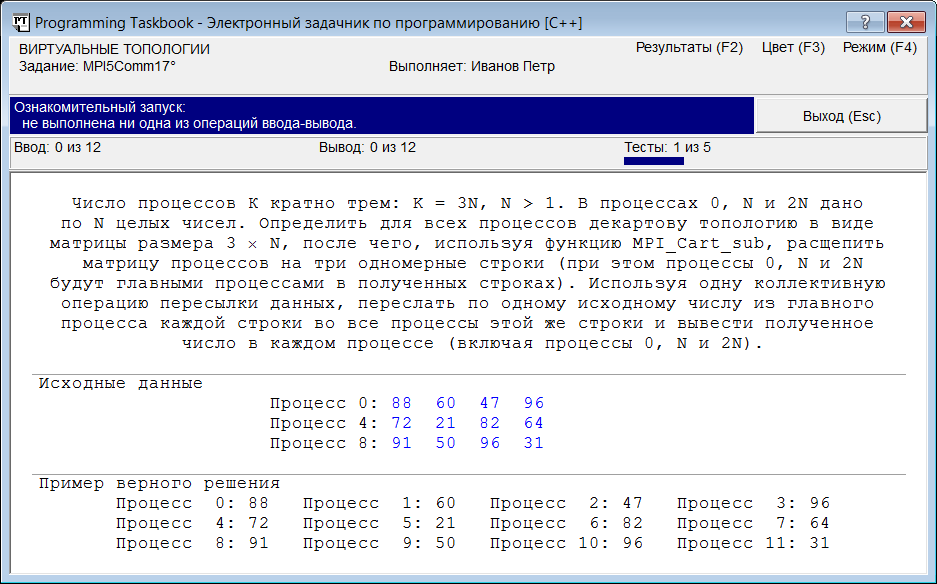
При выполнении параллельной программы каждый процесс может обмениваться данными с любым другим процессом посредством стандартного коммуникатора MPI_COMM_WORLD. Если требуется выделить какую-либо часть имеющихся процессов для организации взаимодействия между ними (например, для коллективного обмена данными в пределах только этой части процессов), то необходимо определить для нужных процессов новый коммуникатор. В предыдущем пункте для создания новых коммуникаторов мы использовали функцию MPI_Comm_split. В библиотеке MPI предусмотрен еще один способ, позволяющий объединить нужные процессы; он состоит в определении для процессов параллельного приложения виртуальной топологии (virtual topology).

Виртуальная топология задает на множестве процессов некоторую структуру, определенным образом упорядочивающую эти процессы. Имеются два вида виртуальной топологии: декартова топология и топология графа. В случае декартовой топологии (Cartesian topology) все процессы интерпретируются как узлы некоторой n-мерной решетки размера k₁ × k₂ × … × k_n (если n = 2, то процессы можно рассматривать как элементы прямоугольной матрицы размера k₁ × k₂). В случае топологии графа (graph topology) процессы интерпретируются как вершины некоторого графа; при этом связи между процессами определяются посредством задания набора ребер (дуг) для этого графа.

Если коммуникатор снабжен виртуальной топологией, то из входящих в него процессов можно выделять различные подмножества регулярной структуры. В частности, из n-мерных решеток, задаваемых с помощью декартовой топологии, можно выделять различные сечения размерности m, где m может меняться от 1 до n – 1 (например, из двумерных матриц можно выделять одномерные строки или столбцы).

Декартова топология: MPI5Comm17

Воспользуемся механизмом виртуальных топологий для выполнения следующего задания.

MPI5Comm17. Число процессов К кратно трем: K = 3N, N > 1. В процессах 0, N и 2N дано по N целых чисел. Определить для всех процессов декартову топологию в виде матрицы размера 3 × N, после чего, используя функцию MPI_Cart_sub, расщепить матрицу процессов на три одномерные строки (при этом процессы 0, N и 2N будут главными процессами в полученных строках). Используя одну коллективную операцию пересылки данных, переслать по одному исходному числу из главного процесса каждой строки во все процессы этой же строки и вывести полученное число в каждом процессе (включая процессы 0, N и 2N).

При ознакомительном запуске этого задания окно задачника примет вид, примерно соответствующий приведенному на следующем рисунке:

Вариант, приведенный в окне, соответствует случаю N = 4: имеется 12 процессов, которые следует интерпретировать как элементы матрицы размера 3 × 4. При этом в процессах, являющихся начальными элементами строк (иначе говоря, в процессах, входящих в первый столбец матрицы), дано по четыре числа, каждое из которых надо переслать в соответствующий процесс этой же строки матрицы процессов.

На первом этапе решения задачи необходимо определить требуемую декартову топологию. Для этого надо использовать функцию MPI_Cart_create, которая имеет следующие параметры:

исходный коммуникатор, для процессов которого определяется декартова топология (в нашем случае MPI_COMM_WORLD);
число размерностей создаваемой декартовой решетки (в нашем случае 2);
целочисленный массив, каждый элемент которого определяет размер по каждому измерению (в нашем случае массив должен состоять из двух элементов со значениями 3 и size/3);
целочисленный массив флагов, определяющих периодичность каждого измерения (в нашем случае достаточно использовать массив из двух нулевых элементов);
целочисленный флаг, определяющий, можно ли среде MPI автоматически менять порядок нумерации процессов (в нашем случае необходимо положить этот параметр равным 0);
результирующий коммуникатор с декартовой топологией (единственный выходной параметр).

Периодичность для некоторых измерений декартовой решетки удобно использовать, например, при выполнении циклического переноса данных между процессами, входящими в эти измерения; в этом случае соответствующий элемент в массиве флагов надо задать отличным от 0.

Автоматическая перенумерация процессов при определении декартовой топологии позволяет учесть физическую конфигурацию компьютерной системы, на которой выполняется параллельная программа, и тем самым повысить эффективность ее выполнения. Однако в учебных программах, выполняемых под управлением задачника PT for MPI-2, порядок процессов в созданных декартовых топологиях должен оставаться неизменным, поэтому перенумерацию процессов следует запретить.

Приведем фрагмент программы, определяющий декартову топологию и связывающий ее с новым коммуникатором comm (этот фрагмент надо поместить в конце функции Solve):

MPI_Comm comm;
int dims[] = {3, size / 3},
  periods[] = {0, 0};
MPI_Cart_create(MPI_COMM_WORLD, 2, dims, periods, 0, &comm);

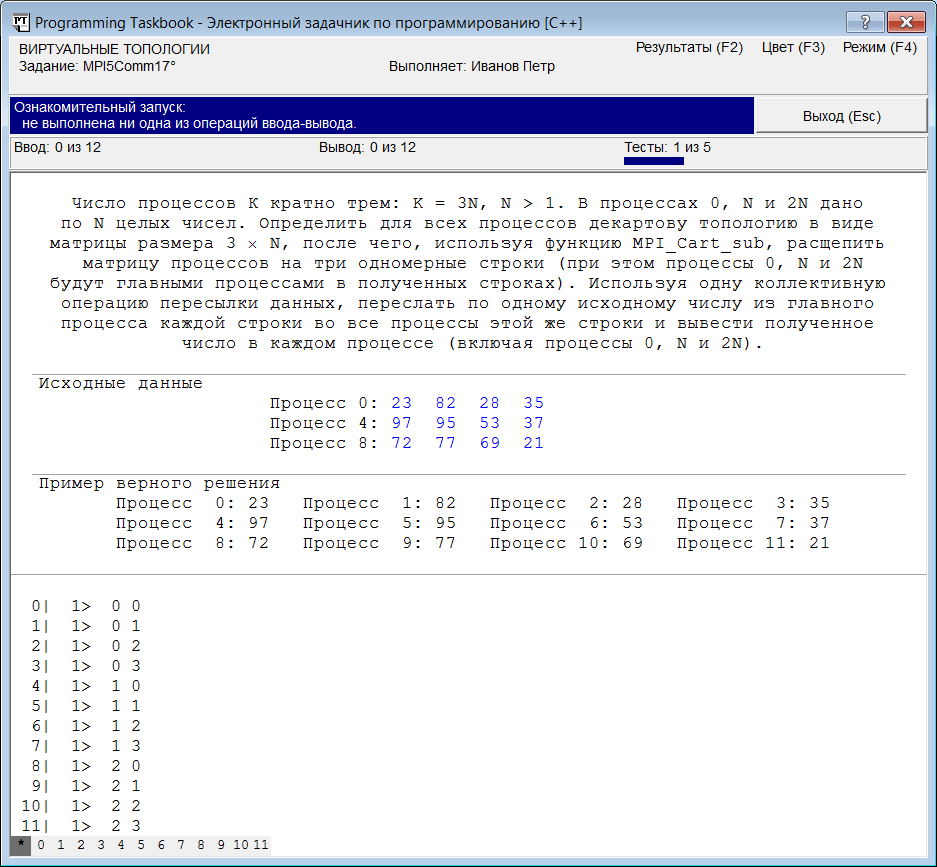
Коммуникатор comm, созданный в результате выполнения функции MPI_Cart_create, будет содержать те же процессы, что и исходный коммуникатор MPI_COMM_WORLD, причем в том же порядке. Однако эти коммуникаторы являются различными. Это проявляется прежде всего в том, что операции пересылки данных, осуществляемые с помощью коммуникаторов MPI_COMM_WORLD и comm, выполняются независимо и не влияют друг на друга (различные коммуникаторы, содержащие один и тот же одинаково упорядоченный набор процессов, называются конгруэнтными; при их сравнении функцией MPI_Comm_compare возвращается результат, равный значению константы MPI_CONGRUENT). Кроме того, с коммуникатором comm дополнительно связана виртуальная топология, а коммуникатор MPI_COMM_WORLD никакой виртуальной топологией не обладает (проверить, связана ли с коммуникатором виртуальная топология определенного типа, можно с помощью функции MPI_Topo_test).

Благодаря наличию декартовой топологии, с каждым процессом коммуникатора comm связывается не только порядковый номер (ранг процесса), но и набор целых чисел, определяющих координаты этого процесса в соответствующей декартовой решетке. Координаты нумеруются от 0.

Координаты процесса в декартовой топологии можно определить по его рангу с помощью функции MPI_Cart_coords (заметим, что функция MPI_Cart_rank позволяет решить обратную задачу). Для выполнения нашего задания использовать функцию MPI_Cart_coords не требуется, однако в ряде случаев (в частности, при отладке параллельных программ) она может оказаться полезной. Поэтому приведем пример ее использования, выведя в раздел отладки окна задачника координаты всех процессов, включенных в декартову решетку. Для этого дополним текст программы следующими операторами:

int coords[2];
MPI_Cart_coords(comm, rank, 2, coords);
Show(coords[0]);
Show(coords[1]);

При запуске дополненной программы окно задачника примет вид, соответствующий приведенному рисунке:

Напомним, что первое число в каждой строке раздела отладки (перед символом «|») обозначает ранг процесса, в котором были выведены данные, указанные в этой строке. Второе число (после которого указывается символ «>») обозначает порядковый номер строки вывода для данного процесса. В нашем случае каждый процесс вывел по одной строке, содержащей два числа: свои координаты в декартовой топологии.

Мы видим, что процесс ранга 0 имеет координаты (0, 0), т. е. является первым элементом первой строки матрицы, а процесс ранга 11 имеет координаты (2, 3), т. е. является последним (четвертым по счету) элементом последней (третьей по счету) строки. Кроме того, в данном случае в первую строку матрицы входят процессы рангов 0, 1, 2, 3, а в первый столбец — процессы рангов 0, 4 и 8.

Вернемся к нашей задаче. Для ее решения необходимо вначале разбить полученную матрицу процессов на отдельные строки, связав с каждой строкой новый коммуникатор. После этого следует выполнить для всех процессов, входящих в одну строку, коллективную операцию MPI_Scatter, рассылающую фрагменты набора данных из одного процесса во все процессы, входящие в коммуникатор.

Расщепление декартовой решетки на набор подрешеток меньшей размерности (в частности, разбиение матрицы на набор строк или столбцов) и связывание с каждой полученной подрешеткой нового коммуникатора выполняется с помощью функции MPI_Cart_sub. В качестве ее первого параметра следует указать исходный коммуникатор с декартовой топологией, в качестве второго — массив флагов, определяющий номера тех измерений, которые должны остаться в подрешетках: если соответствующее измерение должно входить в каждую подрешетку, то на его месте в массиве указывается ненулевой флаг, если же по данному измерению выполняется расщепление исходной решетки, то значение связанного с этим измерением флага должно быть нулевым.

В результате выполнения функции MPI_Cart_sub создается набор новых коммуникаторов, каждый из которых связывается с одной из полученных подрешеток (все созданные коммуникаторы автоматически снабжаются декартовой топологией). Однако возвращается данной функцией (в качестве третьего, выходного параметра) только один из созданных коммуникаторов — тот, в который входит процесс, вызывавший эту функцию. Заметим, что аналогичным образом ведет себя и функция MPI_Comm_split, рассмотренная в предыдущем разделе.

Для разбиения исходной матрицы процессов на набор строк надо в качестве второго параметра функции MPI_Cart_sub указать массив из двух целочисленных элементов, первый из которых равен 0, а второй является ненулевым (например, равен 1). В этом случае все элементы матрицы с одинаковым значением первой (удаляемой) координаты будут объединены в новом коммуникаторе (назовем его comm_sub).

Первый процесс каждой строки (тот, который должен по условию задачи переслать свои данные во все остальные процессы этой же строки) будет иметь в полученном коммуникаторе comm_sub ранг, равный 0. Для определения ранга следует воспользоваться функцией MPI_Comm_rank. После этого, если ранг равен 0, надо прочесть исходные данные и переслать по одному элементу данных каждому процессу этого же коммуникатора, используя функцию MPI_Scatter. В конце останется вывести элемент, полученный каждым процессом.

Приведем завершающую часть решения:

MPI_Comm comm_sub;
int remain_dims[] = {0, 1};
MPI_Cart_sub(comm, remain_dims, &comm_sub);
MPI_Comm_size(comm_sub, &size);
MPI_Comm_rank(comm_sub, &rank);
int b, *a = new int[size];
if (rank == 0)
  for (int i = 0; i < size; ++i)
    pt >> a[i];
MPI_Scatter(a, 1, MPI_INT, &b, 1, MPI_INT, 0, comm_sub);
pt << b;
delete[] a;

Запустив полученную программу, мы получим сообщение о том, что задание выполнено. Удалять фрагмент, обеспечивающий отладочную печать координат процессов, не требуется, так как вывод отладочных данных никак не влияет на проверку правильности решения.

Приведем полный текст полученного решения (без отладочной печати координат):

void Solve()
{
  Task("MPI5Comm17");
  int flag;
  MPI_Initialized(&flag);
  if (flag == 0)
    return;
  int rank, size;
  MPI_Comm_size(MPI_COMM_WORLD, &size);
  MPI_Comm_rank(MPI_COMM_WORLD, &rank);
  MPI_Comm comm;
  int dims[] = {3, size / 3},
    periods[] = {0, 0};
  MPI_Cart_create(MPI_COMM_WORLD, 2, dims, periods, 0, &comm);
  MPI_Comm comm_sub;
  int remain_dims[] = {0, 1};
  MPI_Cart_sub(comm, remain_dims, &comm_sub);
  MPI_Comm_size(comm_sub, &size);
  MPI_Comm_rank(comm_sub, &rank);
  int b, *a = new int[size];
  if (rank == 0)
    for (int i = 0; i < size; ++i)
      pt >> a[i];
  MPI_Scatter(a, 1, MPI_INT, &b, 1, MPI_INT, 0, comm_sub);
  pt << b;
  delete[] a;
}

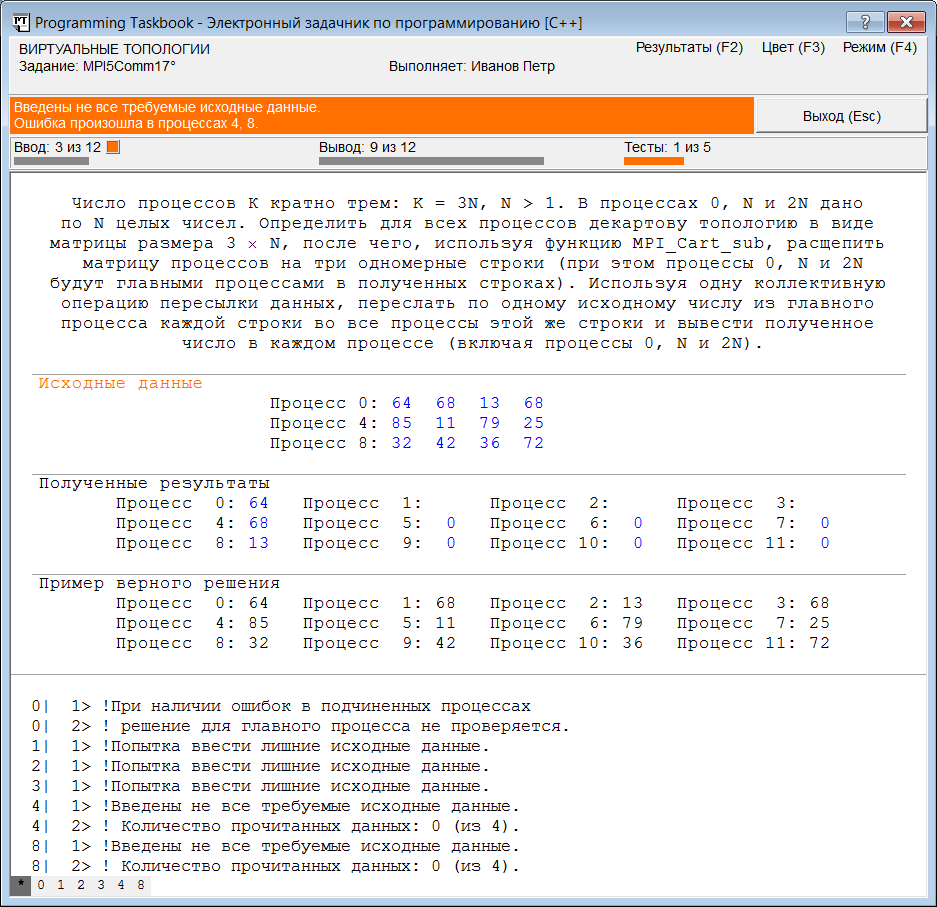
Примечание. Распространенной ошибкой, связанной с использованием функции MPI_Cart_sub, является неправильное указание ее второго параметра — массива флагов. Если, например, в приведенной выше программе поменять местами элементы со значениями 0 и 1 в массиве remain_dims, то при запуске программы в окне задачника будут выведены сообщения об ошибках, подобные приведенным на следующем рисунке:

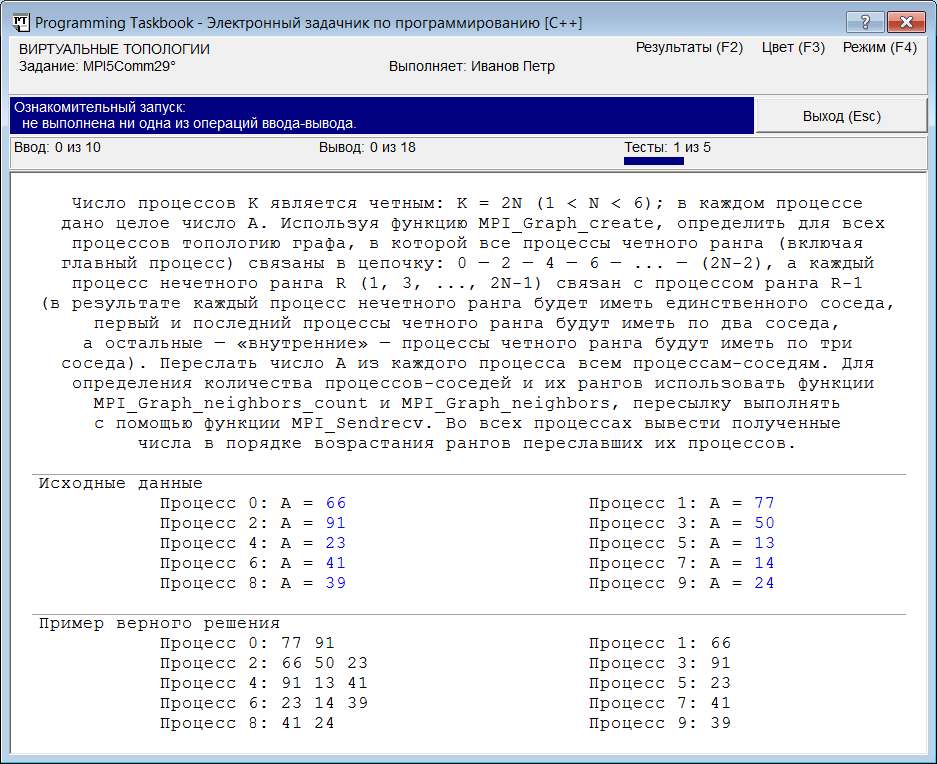
Проанализируем эти сообщения. Из-за неверного указания массива флагов функция MPI_Cart_sub выполнила разбиение исходной матрицы не на строки, а на столбцы; в результате были созданы 4 новых коммуникатора, каждый из которых содержит 3 процесса, входящих в один и тот же столбец матрицы. При этом процесс, являющийся первым в столбце, считается процессом ранга 0 для соответствующего коммуникатора. Поэтому условие в последнем операторе if будет истинным для процессов 0, 1, 2 и 3, и именно для них будут выполняться операторы ввода исходных данных. Однако в процессах 1, 2 и 3 исходных данных не предусмотрено, поэтому при выполнении программы для этих процессов выводится сообщение об ошибке «Попытка ввести лишние исходные данные». С другой стороны, процессы 4 и 8 (являющиеся начальными процессами во второй и третьей строке матрицы) в новых коммуникаторах имеют ненулевой ранг, и поэтому для них ввод данных не выполняется, что и отмечено в сообщении об ошибке для этих процессов: «Введены не все требуемые исходные данные. Количество прочитанных данных: 0 (из 4)». Обратите также внимание на то, что процесс 0 переслал свои исходные данные не в процессы, входящие в первую строку матрицы (как требовалось по условию задачи), а в процессы, входящие в первый столбец. Так как в процессах 1, 2 и 3 исходные данные отсутствовали, в остальные процессы соответствующих столбцов были пересланы нули. Заметим, что в самих процессах 1, 2 и 3 полученные нули не были выведены, так как ранее в каждом из этих процессов задачник выявил ошибку ввода и поэтому заблокировал все последующие операции ввода-вывода для этих процессов. Таким образом, приведенной в окне задачника информации вполне достаточно, чтобы распознать причину ошибки и внести в программу необходимые исправления.

Топология графа: MPI5Comm29

Теперь рассмотрим другой вид виртуальных топологий — топологию графа.

Следует отметить, что для работы с топологиями графа библиотека MPI предоставляет существенно меньше средств, чем для работы с декартовыми топологиями. Напомним, что для процессов, входящих в декартову топологию, можно определить декартовы координаты по их рангам (и ранги по декартовым координатам); кроме того, предусмотрена возможность выделения подрешеток меньшей размерности (причем каждая подрешетка автоматически связывается с новым коммуникатором). Также имеется специальная функция MPI_Cart_shift, позволяющая определить «соседей» процесса вдоль одной из декартовых координат (использование этой функции упрощает пересылку сообщений вдоль указанной координаты). Что же касается топологии графа, то для нее предусмотрена лишь возможность, аналогичная возможности функции MPI_Cart_Shift, а именно определение количества и рангов всех процессов-соседей (neighbors) некоторого процесса в графе, определяемом данной топологией (соседями считаются процессы, связанные ребрами с данным процессом). Познакомимся с этой возможностью на практике, выполнив следующее задание.

MPI5Comm29. Число процессов K является четным: K = 2N (1 < N < 6); в каждом процессе дано целое число A. Используя функцию MPI_Graph_create, определить для всех процессов топологию графа, в которой все процессы четного ранга (включая главный процесс) связаны в цепочку: 0 — 2 — 4 — 6 — … — (2N – 2), а каждый процесс нечетного ранга R (1, 3, …, 2N — 1) связан с процессом ранга R — 1 (в результате каждый процесс нечетного ранга будет иметь единственного соседа, первый и последний процессы четного ранга будут иметь по два соседа, а остальные — «внутренние» — процессы четного ранга будут иметь по три соседа).

Переслать число A из каждого процесса всем процессам-соседям. Для определения количества процессов-соседей и их рангов использовать функции MPI_Graph_neighbors_count и MPI_Graph_neighbors, пересылку выполнять с помощью функции MPI_Sendrecv. Во всех процессах вывести полученные числа в порядке возрастания рангов переславших их процессов.

При ознакомительном запуске этого задания окно задачника примет вид, примерно соответствующий приведенному на рисунке:

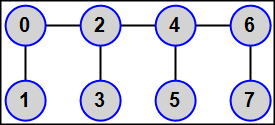
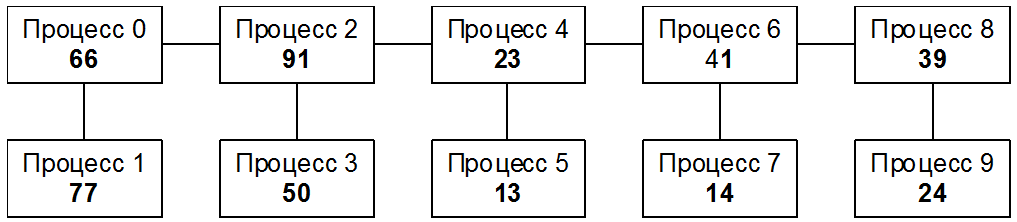
Заметим, что одновременно с окном задачника в правом верхнем углу экрана отобразится рисунок из формулировки задания, иллюстрирующий используемую топологию.

Для большей наглядности изобразим процессы вместе с их исходными данными в виде графа той структуры, которая описана в формулировке задания:

Поскольку процесс ранга 0 имеет двух соседей (процессы ранга 1 и 2), он должен отправить им число 66 и получить от них числа 77 и 91. Процесс ранга 1 имеет только одного соседа (процесс ранга 0), поэтому он должен отправить ему число 77 и получить от него число 66. Процесс ранга 2, имеющий три соседа, должен отправить им число 91 и получить от них числа 66, 50 и 23, и т. д.

Если бы каждый процесс имел информацию о количестве своих соседей, а также об их рангах (в порядке возрастания), то это позволило бы единообразно запрограммировать действия по пересылке данных для любого процесса, независимо от того, сколько соседей он имеет. Требуемая информация о соседях может быть легко получена, если на множестве всех процессов будет определена соответствующая топология графа, а для этого необходимо воспользоваться функцией MPI_Graph_create. Данная функция имеет следующие параметры:

исходный коммуникатор, для процессов которого определяется топология графа;
число вершин графа;
целочисленный массив степеней вершин, i-й элемент которого равен суммарному количеству соседей для первых i вершин графа;
целочисленный массив ребер, содержащий упорядоченный список ребер для всех вершин (вершины нумеруются от 0);
целочисленный флаг, определяющий, можно ли среде MPI автоматически менять порядок нумерации процессов;
результирующий коммуникатор с топологией графа (единственный выходной параметр).

Как и при выполнении предыдущего задания, следует запретить перенумерацию процессов, положив соответствующей флаг равным 0.

Чтобы лучше понять смысл параметров-массивов, задающих характеристики определяемого графа, перечислим их элементы для графа, приведенного на предыдущем рисунке. Первая вершина графа (процесс ранга 0) имеет двух соседей, поэтому первый элемент массива степеней вершин будет равен 2. Вторая вершина графа (процесс ранга 1) имеет одного соседа, поэтому второй элемент массива степеней вершин будет равен 3 (к значению предыдущего элемента прибавляется 1). Третья вершина (процесс ранга 2) имеет трех соседей, поэтому третий элемент массива степеней вершин будет равен 6, и т. д. Получаем следующий набор значений: 2, 3, 6, 7, 10, 11, 14, 15, 17, 18 (предпоследний элемент массива равен 17, так как процесс ранга 8, как и процесс ранга 0, имеет двух соседей). Заметим, что значение последнего элемента массива степеней вершин всегда будет в два раза больше общего количества ребер графа.

В массиве ребер необходимо указать ранги всех соседей для каждой вершины (для большей наглядности будем выделять группы соседей каждой вершины дополнительными пробелами, а сверху в скобках указывать ранг вершины, соседи которой перечислены ниже):

(0)  (1)   (2)   (3)   (4)   (5)   (6)   (7)  (8)  (9)
1 2   0   0 3 4   2   2 5 6   4   4 7 8   6   6 9   8

Размер полученного массива ребер равен значению последнего элемента массива степеней вершин.

Если число процессов равно size, то массив степеней вершин должен содержать size элементов. Размер массива ребер зависит от структуры графа; в нашем случае размер массива ребер равен 2*(size – 1), где size — число процессов.

При заполнении массивов удобно отдельно обработать фрагменты, соответствующие двум первым (ранга 0 и 1) и двум последним (ранга size – 2 и size – 1) вершинам графа, а остальные вершины перебирать в цикле, обрабатывая по две вершины (ранга 2 и 3, 4 и 5, …, size – 4 и size – 3) на каждой итерации.

Следуя описанию функции MPI_Graph_create в стандарте MPI, будем использовать для массива степеней вершин и массива ребер названия index и edges соответственно. При заполнении этих массивов удобно использовать вспомогательную переменную n, равную половине количества процессов. Приведем фрагмент программы, заполняющей массивы index и edges:

int n = size / 2;
int *index = new int[size],
  *edges = new int[2 * (size - 1)];
index[0] = 2;
index[1] = 3;
edges[0] = 1;
edges[1] = 2;
edges[2] = 0;
int j = 3;
for (int i = 1; i <= n - 2; ++i)
{
  index[2 * i] = index[2 * i - 1] + 3;
  edges[j] = 2 * i - 2;
  edges[j + 1] = 2 * i + 1;
  edges[j + 2] = 2 * i + 2;
  index[2 * i + 1] = index[2 * i] + 1;
  edges[j + 3] = 2 * i;
  j += 4;
}
index[2 * n - 2] = index[2 * n - 3] + 2;
index[2 * n - 1] = index[2 * n - 2] + 1;
edges[j] = 2 * n - 4;
edges[j + 1] = 2 * n - 1;
edges[j + 2] = 2 * n - 2;

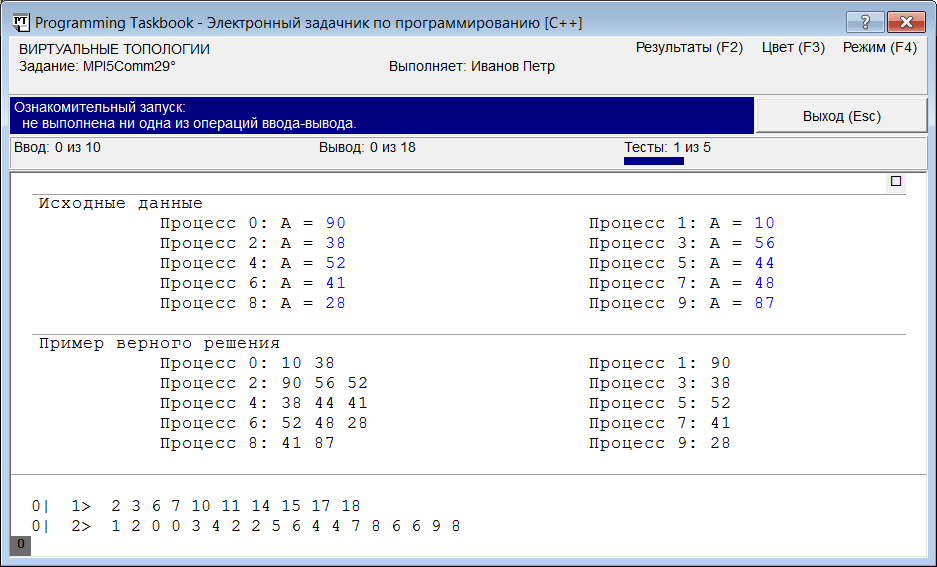
Для проверки правильности данной части алгоритма выведем в раздел отладки окна задачника значения элементов полученных массивов (поскольку эти массивы формируются одинаково во всех процессах, достаточно вывести их значения только в главном процессе):

Если при очередном запуске программы число процессов будет равно 10, то в разделе отладки мы увидим наборы значений, совпадающие с теми, которые были нами получены ранее:

Чтобы уменьшить размеры окна, на приведенном рисунке был скрыт раздел с формулировкой задания. Для этого достаточно нажать клавишу Delete или щелкнуть на маркере, расположенном в правом верхнем углу этого раздела. Повторное нажатие клавиши Delete или щелчок на этом маркере восстанавливает раздел с формулировкой.

Убедившись, что массивы сформированы правильно, создадим топологию графа, вызвав функцию MPI_Graph_create в каждом процессе параллельного приложения:

MPI_Comm g_comm;
MPI_Graph_create(MPI_COMM_WORLD, size, index, edges, 0, &g_comm);

Осталось реализовать завершающую часть алгоритма, непосредственно связанную с пересылкой данных. В этой части для текущего процесса (процесса ранга rank) следует определить количество count его соседей и массив neighbors их рангов в текущей топологии графа (используя функции MPI_Graph_neighbors_count и MPI_Graph_neighbors), после чего организовать обмен данными между текущим процессом и каждым из его соседей (согласно формулировке задания для этого надо использовать функцию MPI_Sendrecv, которая обеспечивает как прием сообщения от некоторого процесса, так и отправку ему другого сообщения).

Приведем завершающую часть решения:

int count;
MPI_Graph_neighbors_count(g_comm, rank, &count);
int *neighbors = new int[count];
MPI_Graph_neighbors(g_comm, rank, count, neighbors);
int a, b;
MPI_Status s;
pt >> a;
for (int i = 0; i < count; ++i)
{
  MPI_Sendrecv(&a, 1, MPI_INT, neighbors[i], 0,
    &b, 1, MPI_INT, neighbors[i], 0, g_comm, &s);
  pt << b;
}
delete[] index;
delete[] edges;
delete[] neighbors;

Запустив полученную программу, мы получим сообщение о том, что задание выполнено.

В заключение данного раздела отметим, что в стандарте MPI-2 появился новый вид топологии графов: топология распределенного графа (distributed graph topology). Ей посвящены два задания, входящие в третью подгруппу группы MPI5Comm.

Разработка сайта:
М. Э. Абрамян, В. Н. Брагилевский

Последнее обновление:
01.01.2024