|
Programming Taskbook |
|
|
||
|
Электронный задачник по программированию |
||||
|
© М. Э. Абрамян (Южный федеральный университет, Университет МГУ-ППИ в Шэньчжэне), 1998–2026 |
|
|
Вычисление сходства строк: Align31 (язык Pascal)В большинстве алгоритмов неточного сравнения строк, описанных в группе Align, можно выделить два этапа: этап восходящей рекурсии, в ходе которого строится вспомогательная матрица, и этап обратного прохода по построенной матрице. После выполнения этапа восходящей рекурсии можно определить числовую характеристику, являющуюся мерой близости сравниваемых строк; это либо варианты редакционного расстояния (см. Align5, Align12, Align18), либо варианты сходства, связанного с глобальным выравниванием (Align31, Align38, Align43, Align48) или выравниванием отдельных частей анализируемых строк (Align53, Align59). В алгоритмах нахождения наибольшей общей подстроки или наибольшей общей подпоследовательности двух строк после построения вспомогательной матрицы можно определить длину общей подстроки (Align63) или, соответственно, общей подпоследовательности (Align67). Рассмотрим задание Align31, посвященное реализации алгоритма восходящей рекурсии для нахождения сходства двух строк, связанного с глобальным оценочным выравниванием. Align31°. Даны строки S1 и S2. Кроме того, дано число m (< 10) — размер алфавита, состоящего из первых строчных латинских букв, и матрица оценок (структура матрицы описана в Align29). Для эффективного вычисления сходства строк V(|S1|, |S2|) по формулам из Align30 можно использовать метод восходящей рекурсии, основанный на последовательном вычислении элементов вспомогательной матрицы V размера (|S1| + 1) × (|S2| + 1) (действия при заполнении матрицы V аналогичны действиям при заполнении матрицы D, описанным в Align5). Элемент, расположенный в последней строчке и последнем столбце матрицы V, определяет значение сходства данных строк. Используя метод восходящей рекурсии, найти матрицу V и вывести элементы ее двух последних строчек: Vn−1, j, j = 0, …, |S2|, Vn, j, j = 0, …, |S2|, где n = |S1|. В формулировке этого задания содержится ряд ссылок на предыдущие задания, в которых вводятся понятия, даются формулы или описываются действия, используемые при реализации требуемого алгоритма. Наличие большого числа подобных ссылок характерно для многих заданий группы Align; это позволяет избежать дублирования определений и формул и тем самым уменьшает размеры формулировок заданий. Кроме того, ссылки дают возможность легко установить связи между рассматриваемыми «родственными» алгоритмами. Для выполнения задания Align31 будем использовать среду Free Pascal Lazarus. Созданная с помощью модуля PT4Load программа-заготовка будет иметь вид: program Align31;
uses PT4;
begin
Task('Align31');
end.
При запуске этой программы на экране появится окно задачника:
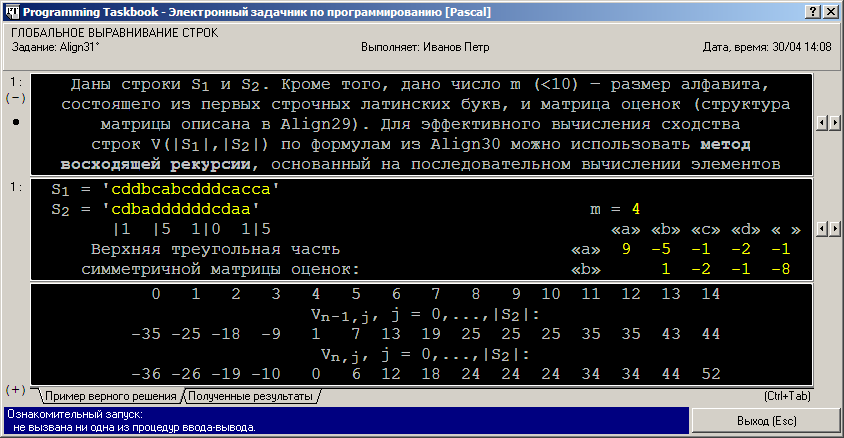
Отметим, что в задании Align31 (как и во многих других заданиях группы Align) раздел исходных данных, подобно разделу с формулировкой задания, допускает прокрутку. Необходимость прокрутки вызвана тем, что для наглядного отображения всех исходных данных, предусмотренных в задании, оказывается недостаточно пяти экранных строк, выделенных для каждого раздела в окне задачника. Кроме двух исходных строк S1 и S2 и числа m, определяющего количество начальных букв латинского алфавита, которые могут входить в исходные строки, в задании приводятся элементы матрицы оценок s, определяющие относительный «вес» пар символов при их выравнивании. Определение матрицы оценок приводится в задании Align29. Это квадратная матрица порядка m + 1; ее строчки и столбцы связываются с различными символами алфавита, используемого в исходных строках, а также с символом пробела (с этим символом связывается последняя строчка и последний столбец матрицы оценок). Во всех заданиях предполагается, что матрица оценок является симметричной, т. е. для любых i и j справедливо равенство si,j = sj,i. Поэтому в наборе исходных данных приводится только верхняя треугольная часть матрицы оценок. Для большей наглядности строчки и столбцы матрицы оценок снабжаются заголовками, содержащими те символы, которым соответствуют данные строчки или столбцы. Приведем вид того же окна, в котором выполнена прокрутка раздела исходных данных, позволяющая отобразить на экране все элементы матрицы оценок:
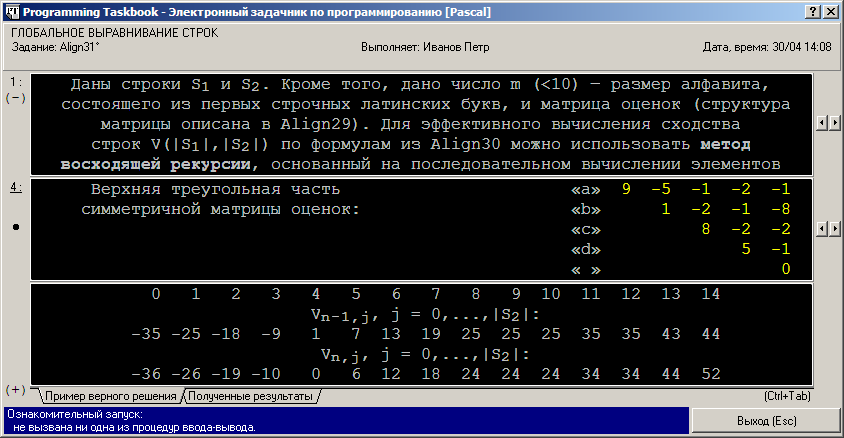
Все диагональные элементы матрицы оценок являются неотрицательными, поскольку они соответствуют весу совпадающих символов в выравнивании. Недиагональные элементы являются отрицательными: это «штрафы» за несовпадение символов или за вставку/удаление символов, т. е. за добавление в выравнивание пробелов. Следует заметить, что последний диагональный элемент матрицы оценок (соответствующий паре пробелов) в алгоритмах выравнивания не используется; он добавлен в набор исходных данных, чтобы в этом наборе действительно была представлена вся верхняя треугольная часть матрицы оценок. В разделе результатов прокрутка не требуется; в нем приведены значения элементов двух последних строчек матрицы V, которая должна быть получена после выполнения этапа восходящей рекурсии. Для большей наглядности в разделе результатов приведены подписи к столбцам полученной матрицы; из этих подписей следует, что столбцы (как и строчки) матрицы нумеруются от 0. Номер последнего столбца равен длине строки S2, а номер последней строчки матрицы — длине строки S1. Последний элемент матрицы (расположенный в ее последней строчке и столбце) равен значению сходства исходных строк. Приступим с реализации алгоритма восходящей рекурсии. Вначале приведем рекуррентные формулы для элементов матрицы V, взяв их из формулировки задания Align30 (знак подчеркивания обозначает символ пробела): • для любого i V(i, 0) = Σk=1,…,is(S1[k], _); Идея метода восходящей рекурсии (описанная в задании Align5 в применении к матрице редакционных расстояний) состоит в последовательном вычислении элементов матрицы по строчкам после предварительного нахождения базовых элементов матрицы, расположенных в ее нулевой строчке и столбце. При этом на этапе вычисления элемента матрицы, расположенного в i-й строчке и j-м столбце уже известны все три элемента, входящие в формулу для Vi,j, а именно элементы, расположенные выше, левее и одновременно выше и левее элемента Vi,j. При программной реализации алгоритма нам потребуются два двумерных массива: для хранения матрицы оценок s (назовем его s0) и для хранения результирующей матрицы V (назовем его v). Будем использовать «обычные» статические массивы языка Pascal. По условию задания значение m не превосходит 9, поэтому максимальный размер матрицы s не может быть больше 10. Размер матрицы V определяется размерами исходных строк S1 и S2. Поскольку в преамбуле к группе Align сказано, что длины исходных строк не превосходят 100, достаточно использовать двумерный массив v, в котором размер по каждому измерению будет равен 101. В качестве нижней границы диапазона индексов удобно использовать значение 0. Для большей наглядности опишем вспомогательную функцию s(c1, c2), которая возвращает значение оценки для пары символов c1 и c2. В этой функции будут вычисляться индексы матрицы s0, соответствующие символам c1 и c2, после чего будет возвращаться значение элемента матрицы s0 с этими индексами. Для вычисления индексов воспользуемся еще одной вспомогательной функцией (назовем ее CharToInd). Учитывая приведенные выше замечания, получаем следующий вариант решения (напомним, что для ввода строковых и целочисленных данных надо использовать процедуры GetS и GetN соответственно, а для вывода целочисленных данных — процедуру PutN): program Align31;
uses PT4;
var s0: array[0..9, 0..9] of integer;
s1, s2: string;
m, n, p, i, j, k, max: integer;
v: array[0..100, 0..100] of integer;
function CharToInd(c: char): integer;
begin
if c = ' ' then
result := m
else
result := Ord(c) - Ord('a');
end;
function s(c1, c2: char): integer;
begin
result := s0[CharToInd(c1), CharToInd(c2)];
end;
begin
Task('Align31');
// ввод исходных данных
GetS(s1);
GetS(s2);
GetN(m);
for i := 0 to m do
begin
GetN(s0[i,i]);
for j := i+1 to m do
begin
GetN(s0[i,j]);
s0[j,i] := s0[i,j];
end;
end;
n := length(s1);
p := length(s2);
// вычисление базовых элементов матрицы V
v[0,0] := 0;
for i := 1 to n do
v[i,0] := v[i-1,0] + s(s1[i], ' ');
for j := 1 to p do
v[0,j] := v[0,j-1] + s(' ', s2[j]);
// восходящая рекурсия
for i := 1 to n do
for j := 1 to p do
begin
max := v[i-1,j] + s(s1[i], ' ');
k := v[i,j-1] + s(' ', s2[j]);
if k > max then
max := k;
k := v[i-1,j-1] + s(s1[i], s2[j]);
if k > max then
max := k;
v[i,j] := max;
end;
// вывод результатов
for j := 0 to p do
PutN(v[n-1,j]);
for j := 0 to p do
PutN(v[n,j]);
end.
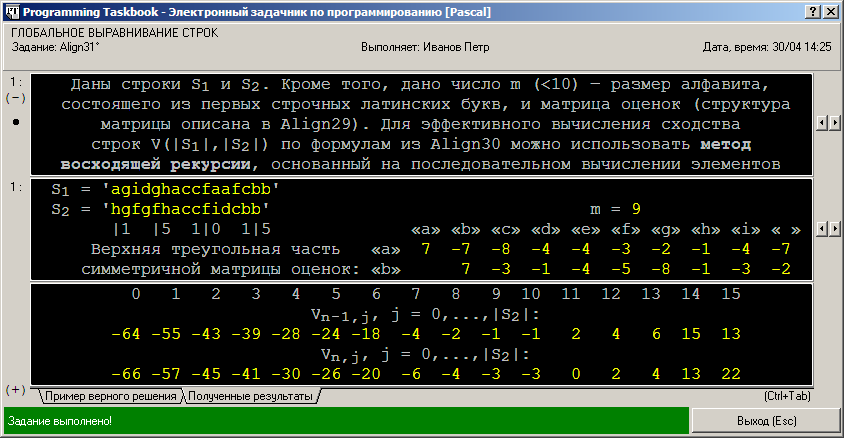
При реализации функции CharToInd было учтено, что строчные латинские буквы располагаются в кодовой таблице последовательно, т. е. имеют последовательные коды, поэтому для определения индекса, соответствующего некоторой букве в матрице оценок, достаточно вычесть из кода этой буквы (определяемого с помощью стандартной функции Ord) код символа «а». Символ пробела обрабатывается отдельно; ему соответствует индекс m — последний индекс в матрице оценок при нумерации индексов от 0. Следует обратить внимание на заполнение матрицы s0: во вложенном цикле диапазон изменения параметра внутреннего цикла j зависит от текущего значения параметра внешнего цикла i; это обеспечивает перебор всех элементов, соответствующих верхней треугольной части матрицы. Для того чтобы в дальнейшем можно было обращаться к любому элементу матрицы, после ввода очередного недиагонального элемента матрицы s0 заполняется и элемент, симметричный ему относительно главной диагонали: s0[j,i] := s0[i,j] (для диагональных элементов это действие не выполняется). При вычислении и выводе матрицы v используются вспомогательные переменные n и p, равные длине строк s1 и s2 соответственно. После пяти запусков полученной программы будет выведено сообщение о том, что задание выполнено:
Примечание. Расширение языка Pascal, реализованное в системах Delphi, Lazarus и PascalABC.NET, позволяет использовать в программах динамические массивы, в том числе многомерные. В нашем случае динамический массив целесообразно использовать для хранения матрицы v; это дает возможность существенно уменьшить ее размер в случае, когда исходные строки имеют небольшую длину. Динамические массивы всегда индексируются от 0, что соответствует индексации, использованной в нашей программе. Для возможности работы с массивом v как двумерным динамическим массивом необходимо изменить его описание, а также выполнить инициализацию, указав размер массива по каждому измерению. Описание двумерного динамического массива v должно иметь следующий вид: var v: array of array of integer; Размеры массива v определяются по значениям n и p — длинам исходных строк. Приведенный ниже код должен быть помещен перед комментарием «вычисление базовых элементов матрицы V»: SetLength(v, n+1);
for i := 0 to n do
SetLength(v[i], p+1);
В этом фрагменте вначале задается количество строчек матрицы, после чего в цикле определяется размер каждой строчки. Остальные разделы программы модификации не требуют. |
|
|
Разработка сайта: |
Последнее обновление: |