Programming Taskbook

Электронный задачник по программированию

©  М. Э. Абрамян (Южный федеральный университет, Университет МГУ-ППИ в Шэньчжэне), 1998–2024

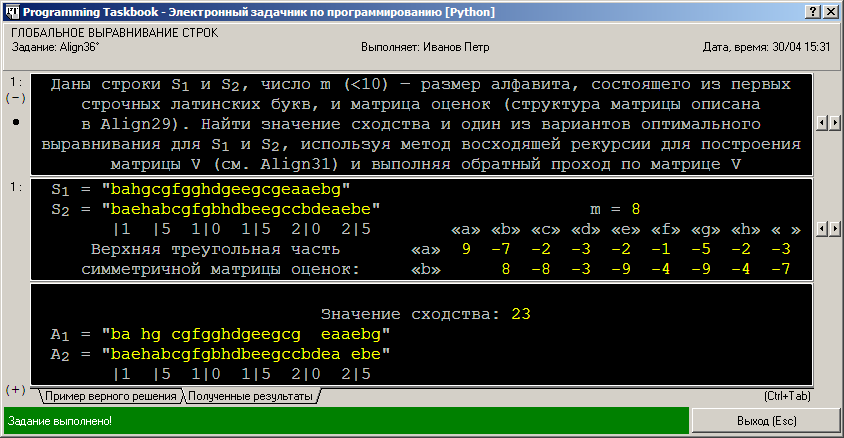
Полный вариант алгоритма оптимального выравнивания: Align36 (язык Python)

Для каждого алгоритма, описанного в группе Align, предусмотрены итоговые задания, в которых требуется реализовать этот алгоритм в полном объеме. В итоговых заданиях необходимо построить вспомогательную матрицу, используя метод восходящей рекурсии, после чего выполнить обратный проход по данной матрице для определения требуемой характеристики, связанной с сопоставлением строк. Таковы задания Align10–11, Align16–17, Align22–23 на определение оптимального редакционного предписания, Align36–37, Align41–42, Align46–47, Align51–52 на построение глобального выравнивания, Align57–58 на определение приближенных вхождений одной строки в другую, Align62 на локальное выравнивание строк, Align65 и Align69 на нахождение наибольшей общей подстроки и наибольшей общей подпоследовательности соответственно.

В качестве примера подобного задания рассмотрим задание Align36, выполнив его на языке Python.

Align36°. Даны строки S₁ и S₂, число m (< 10) — размер алфавита, состоящего из первых строчных латинских букв, и матрица оценок (структура матрицы описана в Align29). Найти значение сходства и один из вариантов оптимального выравнивания для S₁ и S₂, используя метод восходящей рекурсии для построения матрицы V (см. Align31) и выполняя обратный проход по матрице V (см. Align33). Выбор варианта оптимального выравнивания выполнять по правилам, описанным в Align34.

В обсуждении деталей реализации алгоритма нет необходимости, поскольку оба его этапа были подробно рассмотрены в примерах выполнения задания Align31 и задания Align35. Следует обратить внимание лишь на правило выбора варианта оптимального выравнивания, приведенное в Align34 и состоящее в следующем: если для некоторого элемента V_i,j возможны перемещения более чем в один из его соседних элементов V_i,j–1, V_i–1,j, V_i–1,j–1, то предпочтение отдается перемещению влево (соответствующему вставке пробела в первую строку), а при его невозможности — перемещению вверх (соответствующему вставке пробела во вторую строку).

Первый вариант решения представляет собой простое объединение алгоритмов ранее рассмотренных алгоритмов (см. примеры решений Align31 и Align35), записанное на языке Python. Заметим, что, поскольку в задании Align36 не требуется находить все варианты оптимального выравнивания, этап обратного прохода можно реализовать без вспомогательной рекурсивной функции. Для хранения элементов матрицы оценок s и матрицы V используются списки s0 и v соответственно, элементами которых, в свою очередь, также являются списки. Для нахождения максимального из трех значений достаточно вызвать стандартную функцию max с тремя аргументами. Напомним, что для ввода данных любого типа в программе на языке Python, использующей задачник, предназначена универсальная функция get, а для вывода результатов — функция put.

    # -*- coding: cp1251 -*-
    from pt4 import *
    task("Align36")
    s1 = get()
    s2 = get()
    m = get()
    n = len(s1)
    p = len(s2)

    # формирование и заполнение матрицы оценок
    s0 = (m+1)*[0]
    for i in range(m+1):
        s0[i] = (m+1)*[0]
    for i in range(m+1):
        s0[i][i] = get()
        for j in range(i+1, m+1):
            s0[i][j] = get()
            s0[j][i] = s0[i][j]

    def chartoind(c):
        if c == " ":
            return m
        return ord(c) - ord("a")
    def s(c1, c2):
        return s0[chartoind(c1)][chartoind(c2)]

    # формирование и заполнение матрицы V
    v = (n+1)*[0]
    for i in range(n+1):
        v[i] = (p+1)*[0]
    v[0][0] = 0
    for i in range(1, n+1):
        v[i][0] = v[i-1][0] + s(s1[i-1], " ")
    for j in range(1, p+1):
        v[0][j] = v[0][j-1] + s(" ", s2[j-1])
    for i in range(1, n+1):
        for j in range(1, p+1):
            v[i][j] = max(v[i-1][j] + s(s1[i-1], " "), \
                          v[i][j-1] + s(" ", s2[j-1]), \
                          v[i-1][j-1] + s(s1[i-1], s2[j-1]))

    # вывод значения сходства s1 и s2
    put(v[n][p])

    # обратный проход по v для нахождения выравнивания (a1, a2)
    a1 = ""
    a2 = ""
    i = n
    j = p
    while i+j > 0:
        if i == 0:
            a1 = " " + a1
            a2 = s2[j-1] + a2
            j -= 1
        elif j == 0:
            a1 = s1[i-1] + a1
            a2 = " " + a2
            i -= 1
        elif v[i][j] == v[i][j-1] + s(" ",s2[j-1]):
            a1 = " " + a1
            a2 = s2[j-1] + a2
            j -= 1
        elif v[i][j] == v[i-1][j] + s(s1[i-1],' '):
            a1 = s1[i-1] + a1
            a2 = " " + a2
            i -= 1
        else:
            a1 = s1[i-1] + a1
            a2 = s2[j-1] + a2
            i -= 1
            j -= 1
    put(a1, a2)

После требуемого количества тестовых запусков в окне задачника будет выведено сообщение о том, что задание выполнено:

Реализацию этапа обратного прохода по матрице V можно упростить, если на этапе восходящей рекурсии сохранять дополнительную информацию о том, какой из соседних элементов использовался для определения значения элемента V_i,j. Эту информацию можно сохранять, например, во вспомогательной матрице b с элементами-кортежами с двумя полями: di — смещение по строкам и dj — смещение по столбцам. Например, если элемент V_i,j был определен по элементу V_i,j–1, то значение b[i][j] равно (0, 1) (смещение по i отсутствует, смещение по j равно 1), а если элемент V_i,j был определен по элементу V_i–1,j, то b[i][j] равен (1, 0). Очевидно, b[i][0] = (1, 0), а b[0][j] = (0, 1). Если максимум в формуле для V_i,j достигается для нескольких соседних элементов, то значение b[i][j] определяется в соответствии с ранее рассмотренным правилом выбора варианта выравнивания.

Приведем соответствующий вариант решения, начиная с этапа восходящей рекурсии (предыдущая часть программы не изменится):

    # формирование и заполнение матрицы V
    v = (n+1)*[0]
    b = (n+1)*[0]
    for i in range(n+1):
        v[i] = (p+1)*[0]
        b[i] = (p+1)*[0]
    v[0][0] = 0
    for i in range(1,n+1):
        v[i][0] = v[i-1][0] + s(s1[i-1], " ")
        b[i][0] = (1, 0)
    for j in range(1,p+1):
        v[0][j] = v[0][j-1] + s(" ", s2[j-1])
        b[0][j] = (0, 1)
    for i in range(1,n+1):
        for j in range(1,p+1):
            max = v[i-1][j] + s(s1[i-1], " ")
            b0 = (1, 0)
            k = v[i][j-1] + s(" ", s2[j-1])
            if k > max:
                max = k
                b0 = (0, 1)
            k = v[i-1][j-1]+s(s1[i-1], s2[j-1])
            if k > max:
                max = k
                b0 = (1, 1)
            v[i][j] = max
            b[i][j] = b0

    # вывод значения сходства s1 и s2
    put(v[n][p])

    # обратный проход для нахождения выравнивания (a1,a2)
    a1 = ""
    a2 = ""
    i = n
    j = p
    while i+j > 0:
        di, dj = b[i][j]
        if di == 0:
            a1 = " " + a1
        else:
            a1 = s1[i-1] + a1
            i -= 1
        if dj == 0:
            a2 = " " + a2
        else:
            a2 = s2[j-1] + a2
            j -= 1
    put(a1, a2)

В данном варианте решения несколько усложнился этап восходящей рекурсии (за счет дополнительного вычисления элементов матрицы b), однако существенно упростился этап обратного прохода. Заметим, что этап обратного прохода можно упростить еще больше, если в матрице b хранить не только смещения по строкам и столбцам, но и символы c1 и с2, которые требуется добавлять к строкам a1 и a2 на каждом шаге.

Описанная модификация алгоритма может использоваться и при нахождении всех различных вариантов выравнивания. В этом случае каждый элемент b[i][j] вспомогательной матрицы b должен содержать список кортежей, при этом размер списка, равный 1, 2 или 3, зависит от количества способов, которыми можно перейти от элемента V_i,j к одному из соседних элементов при выполнении обратного прохода.

Разработка сайта:
М. Э. Абрамян, В. Н. Брагилевский

Последнее обновление:
01.01.2024