Programming Taskbook

Электронный задачник по программированию

©  М. Э. Абрамян (Южный федеральный университет, Университет МГУ-ППИ в Шэньчжэне), 1998–2024

Обратный ход в алгоритме оптимального выравнивания: Align35 (язык C++)

В данном примере описывается один из вариантов реализации обратного прохода по матрице, полученной методом восходящей рекурсии. Обратный проход используется для нахождения какого-либо варианта (или всех вариантов) оптимального редакционного предписания (Align7–9, Align14–15, Align20–21), глобального выравнивания (Align33–35, Align39–40, Align44–45, Align49–50), приближенного вхождения одной строки в другую (Align55–56), локального выравнивания (Align60–61), наибольшей общей подстроки (Align64–65), наибольшей общей подпоследовательности (Align68). Особенностью перечисленных заданий является то, что в них не требуется предварительно выполнять этап восходящей рекурсии, поскольку матрица, необходимая для реализации обратного прохода, предоставляется в составе набора исходных данных.

Рассмотрим задание Align35, связанное с нахождением всех вариантов оптимального оценочного выравнивания (это задание входит в ту же серию, что и рассмотренное в предыдущем примере задание Align31):

Align35°. Даны строки S₁ и S₂, число m (< 10) — размер алфавита, состоящего из первых строчных латинских букв, и матрица оценок (структура матрицы описана в Align29). Кроме того, дана матрица V, полученная методом восходящей рекурсии (см. Align31). Найти все варианты оптимального выравнивания для S₁ и S₂, выполняя обратный проход по матрице V (см. Align33). Если для некоторого элемента V_i,j возможны перемещения более чем в один из его соседних элементов V_i,j−1, V_i−1,j, V_i−1,j−1, то использовать следующий порядок перебора допустимых в данной позиции действий: вставка пробела в первую строку и текущего символа во вторую строку (перемещение влево), вставка пробела во вторую строку и текущего символа в первую строку (перемещение вверх), вставка текущих символов в обе строки (перемещение по диагонали). Реализовать один шаг обратного хода в виде рекурсивной функции, количество собственных вызовов которой зависит от числа возможных перемещений в соседние элементы. Вывести все найденные оптимальные выравнивания.

В задании требуется реализовать наиболее сложный вид обратного прохода, предназначенный для нахождения всех различных вариантов оптимального оценочного выравнивания. Обратный проход описан в задании Align33; он состоит в перемещении из правого нижнего элемента матрицы V в ее левый верхний элемент, причем на шаге, который начинается в элементе матрицы V_i,j, перемещение должно выполняться в тот из элементов V_i,j–1, V_i–1,j, V_i–1,j–1, на котором достигается максимум в формуле для V(i, j):

V(i, j) = max{V(i − 1, j) + s(S₁[i], _), V(i, j − 1) + s(_, S₂[j]), V(i − 1, j − 1) + s(S₁[i], S₂[j])}.

Если максимум в формуле достигается для нескольких входящих в нее выражений, то на данном шаге можно переместиться в любой из элементов, соответствующих этим выражениям.

Для элемента, расположенного в нулевой строке, перемещение всегда выполняется влево, а для элемента, расположенного в нулевом столбце, перемещение выполняется вверх.

На каждом шаге обратного прохода дополняются строки A₁ и A₂; после завершения алгоритма в них будет храниться оптимальное оценочное выравнивание исходных строк S₁ и S₂, т. е. выравнивание, для которого сумма оценок символов с одинаковыми номерами (s(A₁[1], A₂[1]), s(A₁[2], A₂[2]) и т. д.) будет максимальной (и равной значению сходства строк S₁ и S₂). Способ дополнения зависит от направления перемещения: если выполняется перемещение влево (из V_i,j в V_i,j–1), то к строке A₁ слева приписывается пробел, а к строке A₂ — символ S₂[j]; если выполняется перемещение вверх (из V_i,j в V_i–1,j), то к строке A₁ слева приписывается символ S₁[i], а к строке A₂ — пробел; наконец, если перемещение выполняется по диагонали (из V_i,j в V_i–1,j–1), то к строке A₁ слева приписывается символ S₁[i], а к строке A₂ — символ S₂[j]. Если на некотором шаге имеется несколько вариантов перемещения (например, либо влево, либо вверх), то каждому из этих вариантов будет соответствовать один из способов дополнения строк A₁ и A₂; в результате будут получены различные варианты оптимального выравнивания исходных строк.

Задание будем выполнять на языке C++ в среде Microsoft Visual Studio .NET 2010. Программа-заготовка для данного задания имеет вид:

    #include "pt4.h"
    using namespace std;

    void Solve()
    {
        Task("Align35");

    }

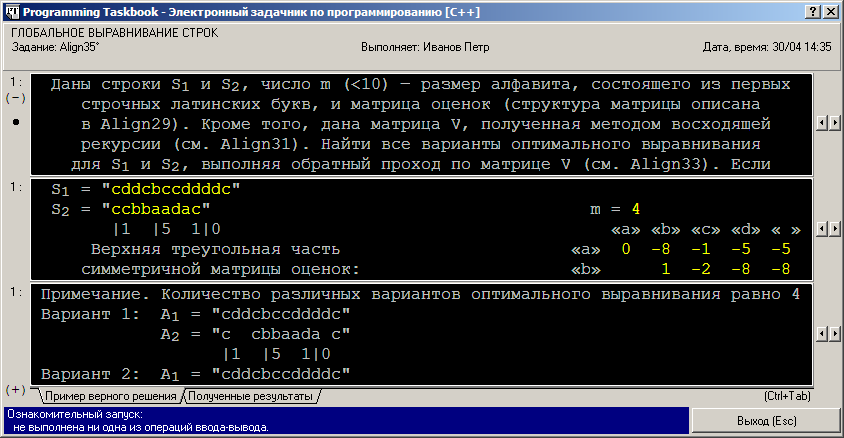
После запуска созданной программы на экране появится окно задачника с формулировкой задания, вариантом исходных данных и примером правильного решения:

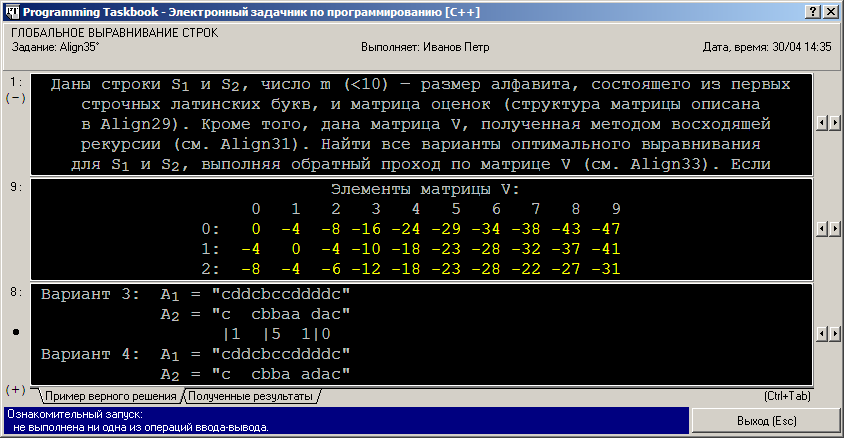
В данном окне прокрутка доступна для всех разделов: и для формулировки задания, и для набора исходных данных, и для набора результатов.

В разделе исходных данных, помимо двух исходных строк S₁ и S₂, размера алфавита m и верхней треугольной части матрицы оценок s (эти элементы исходных данных были подробно описаны при рассмотрении задания Align31), содержатся все элементы матрицы V, вычисленные самим задачником при инициализации задания. Для большей наглядности строчки и столбцы матрицы V в разделе исходных данных снабжены подписями — порядковыми номерами, начиная от 0:

Размер матрицы V определяется длиной строк S₁ и S₂: число ее строчек равно |S₁| + 1, а число столбцов равно |S₂| + 1.

В разделе результатов приводятся все различные варианты оптимального выравнивания исходных строк. Начальная строка раздела содержит примечание, в котором указывается количество вариантов; для приведенного на рисунке набора результатов оно равно 4 (выводить это количество при выполнении задания не требуется). Затем выводятся пары найденных выравниваний, снабженные линейками, которые позволяют быстро определить номера позиций символов. С помощью прокрутки можно одновременно отобразить на экране два соседних варианта выравнивания (на рисунке показаны варианты выравнивания с номерами 3 и 4).

Приступим к выполнению задания. Его особенность состоит в том, что требуется найти все варианты выравнивания, причем количество вариантов заранее неизвестно. В этой ситуации удобно использовать рекурсивный алгоритм, кратко описанный в заключительной части формулировки задания: один шаг обратного прохода оформляется в виде рекурсивной функции (назовем эту функцию step), которая определяет допустимые направления для последующего шага и вызывает себя для каждого допустимого направления. В качестве параметров этой функции будем передавать позицию текущего шага (i, j), а также сформированные к этому времени части строк A₁ и A₂. Рекурсивные вызовы завершаются при попадании в позицию (0, 0); при этом выводится найденный вариант выравнивания — строки A₁ и A₂. Преимуществом данного алгоритма является то, что в нем не требуется предварительно определять количество различных вариантов выравнивания и выделять для них память, поскольку каждый экземпляр выполняющейся рекурсивной функции «помнит» тот вариант выравнивания, с которым он работает.

При реализации рекурсивной функции step удобно использовать вспомогательные функции s(char c1, char c2) и chartoind(char c), аналогичные тем, которые были реализованы при выполнении задания Align31. Для хранения матрицы оценок можно использовать массив s0[10][10]. Для матрицы V память целесообразно выделять после определения длины исходных строк s1 и s2, поэтому соответствующая переменная v будет описываться как int**; при этом действия по выделению памяти будут аналогичны действиям, описанным в примечании к примеру выполнения задания Align31.

При программной реализации формул необходимо учитывать, что символы в строках языка C++ индексируются от 0.

Вывод полученных результатов будет производиться непосредственно в рекурсивной функции step, поэтому завершающим оператором функции Solve будет стартовый вызов этой функции с параметрами n (длина строки s1), p (длина строки s2) и двумя пустыми строками, к которым в дальнейшем будут приписываться символы, входящие в оптимальное выравнивание. Напомним, что для ввода и вывода данных в программе, использующей задачник, предназначен поток ввода-вывода pt.

Получаем следующий вариант решения:

    #include "pt4.h"
    using namespace std;

    string s1, s2;
    int m;
    int s0[10][10];
    int** v;

    int chartoind(char c)
    {
        return c == ' ' ? m : (int)c - (int)'a';
    }

    int s(char c1, char c2)
    {
        return s0[chartoind(c1)][chartoind(c2)];
    }

    void step(int i, int j, string a1, string a2)
    {
        if (i+j == 0)
            pt << a1 << a2;
        else if (i == 0)
            step(i, j-1, ' ' + a1, s2[j-1] + a2);
        else if (j == 0)
            step(i-1, j, s1[i-1] + a1, ' ' + a2);
        else
        {
            if (v[i][j] == v[i-1][j-1] + s(s1[i-1], s2[j-1]))
                step(i-1, j-1, s1[i-1] + a1, s2[j-1] + a2);
            if (v[i][j] == v[i-1][j] + s(s1[i-1], ' '))
                step(i-1, j, s1[i-1] + a1, ' ' + a2);
            if (v[i][j] == v[i][j-1] + s(' ', s2[j-1]))
                step(i, j-1, ' ' + a1, s2[j-1] + a2);
        }
    }

    void Solve()
    {
        Task("Align35");
        pt >> s1 >> s2 >> m;
        int n = s1.length(), p = s2.length();
        for (int i = 0; i < m+1; i++)
        {
            pt >> s0[i][i];
            for (int j = i+1; j < m+1; j++)
            {
                pt >> s0[i][j];
                s0[j][i] = s0[i][j];
            }
        }
        v = new int*[n+1];
        for (int i = 0; i < n+1; i++)
        {
            v[i] = new int[p+1];
            for (int j = 0; j < p+1; j++)
                pt >> v[i][j];
        }
        step(n, p, "", "");
    }

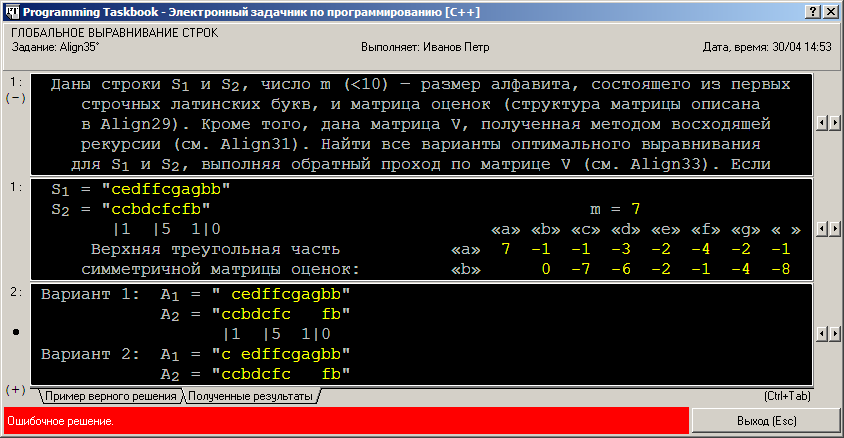
В функции step отдельно обрабатываются особые ситуации i = 0 и j = 0, в которых не требуется выполнять дополнительные проверки.

Приведенная программа содержит недочет, из-за которого это решение не будет считаться правильным, хотя в нем действительно находятся все различные варианты оптимального выравнивания:

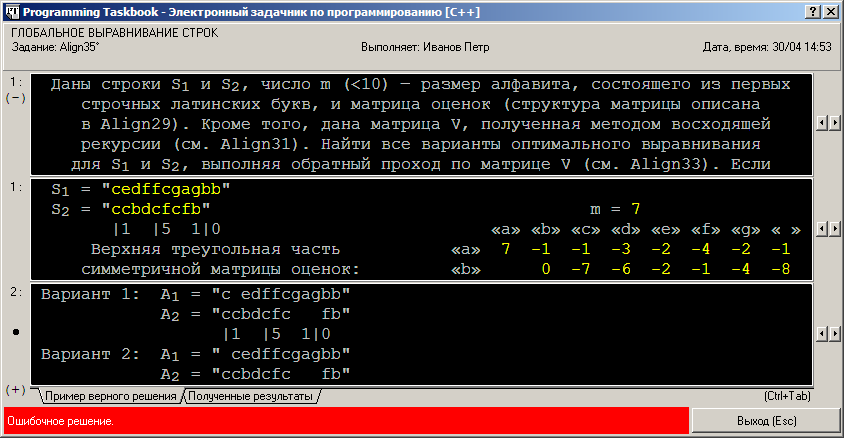
Причина сообщения об ошибке заключается в том, что найденные оптимальные выравнивания выводится не в том порядке, который требуется по условию задания. В этом можно убедиться, перейдя на вкладку «Пример верного решения»:

Для того чтобы обеспечить вывод результатов в нужном порядке, необходимо обратить внимание на ту часть формулировки задания, в которой говорится о порядке перебора вариантов при реализации обратного хода: вначале должно обрабатываться перемещение влево, затем перемещение вверх, затем — перемещение по диагонали. Таким образом, завершающий фрагмент функции step надо изменить следующим образом:

    if (v[i][j] == v[i][j-1] + s(' ', s2[j-1]))
        step(i, j-1, ' ' + a1, s2[j-1] + a2);
    if (v[i][j] == v[i-1][j] + s(s1[i-1], ' '))
        step(i-1, j, s1[i-1] + a1, ' ' + a2);
    if (v[i][j] == v[i-1][j-1] + s(s1[i-1], s2[j-1]))
        step(i-1, j-1, s1[i-1] + a1, s2[j-1] + a2);

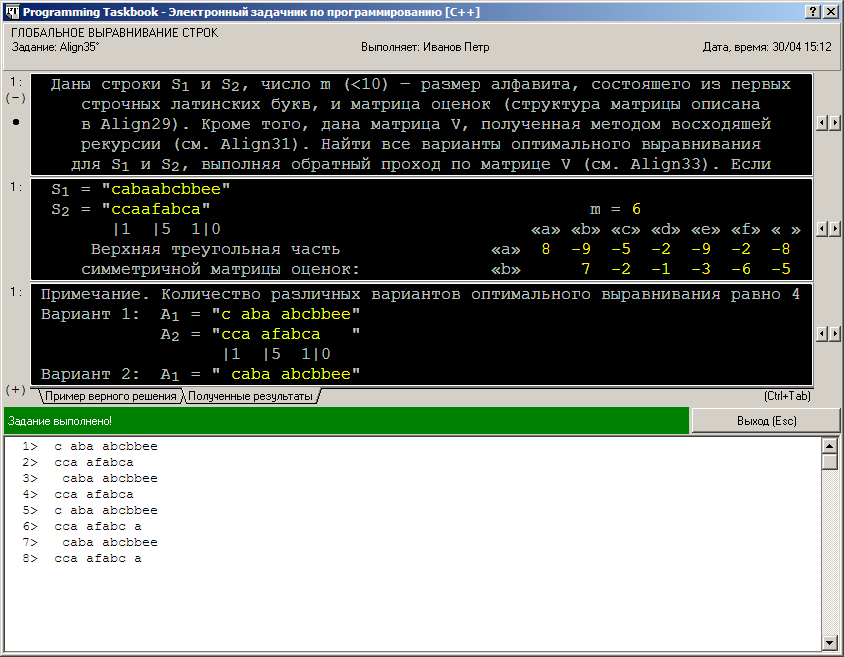
После пяти запусков исправленной программы будет выведено сообщение о том, что задание выполнено.

Завершая обсуждение данного задания, отметим, что при его выполнении (и выполнении аналогичных заданий) часто бывает удобно одновременно отображать на экране все найденные результаты. Для этого достаточно организовать дополнительный вывод результатов в разделе отладки, используя функцию ShowLine. В нашем случае следует дополнить начальную часть функции step двумя вызовами функции ShowLine:

    if (i+j == 0)
    {
        pt << a1 << a2;
        ShowLine(a1);
        ShowLine(a2);
    }

Приведем вид окна при запуске дополненной программы:

Разработка сайта:
М. Э. Абрамян, В. Н. Брагилевский

Последнее обновление:
01.01.2024