Programming Taskbook

Электронный задачник по программированию

©  М. Э. Абрамян (Южный федеральный университет, Университет МГУ-ППИ в Шэньчжэне), 1998–2024

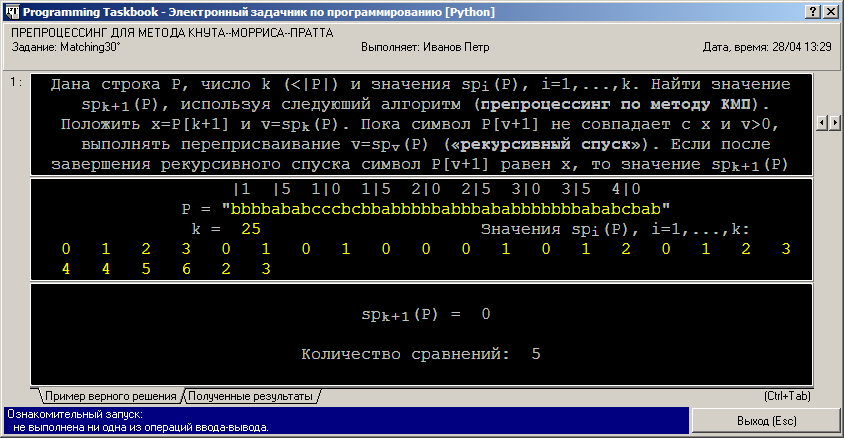
Препроцессинг для метода Кнута–Морриса–Пратта: Match30 (язык Python)

Язык Python в настоящее время становится все более популярным при обучении программированию; кроме того, он широко используется в биоинформатике (имеется даже специализированный комплекс библиотек BioPython). Поэтому следующий пример, связанный с алгоритмом препроцессинга в методе Кнута–Морриса–Пратта, мы рассмотрим для данного языка.

Match30°. Дана строка P, число k (< |P|) и значения sp_i(P), i = 1, …, k. Найти значение sp_k+1(P), используя следующий алгоритм (препроцессинг по методу КМП). Положить x = P[k + 1] и v = sp_k(P). Пока символ P[v + 1] не совпадает с x и v > 0, выполнять переприсваивание v = sp_v(P) («рекурсивный спуск»). Если после завершения рекурсивного спуска символ P[v + 1] равен x, то значение sp_k+1(P) положить равным v + 1, в противном случае sp_k+1(P) = 0. Вывести значение sp_k+1(P) и количество сравнений символов, потребовавшееся при выполнении алгоритма.

Примечание. В алгоритме фактически требуется найти P' — наибольший собственный префикс подстроки P[1..k], который совпадает с суффиксом P[1..k] и за которым (в позиции |P'|+1) следует символ x. Первый шаг алгоритма почти очевиден: если x совпадает с символом P[sp_k(P) + 1], то sp_k+1(P) ≥ sp_k(P) + 1, и достаточно доказать, что оценка sp_k+1(P) > sp_k(P) + 1 никогда не выполняется (доказывается от противного). Отсутствие совпадения равносильно оценке sp_k+1(P) ≤ sp_k(P). Используя эту оценку, можно доказать, что искомая строка P' представляет собой наибольший собственный префикс P'' подстроки P[1..sp_k(P)], который совпадает с суффиксом P[1..k] и за которым (в позиции |P''| + 1) следует символ x. Сравнивая данное утверждение с первым предложением настоящего примечания, получаем алгоритм рекурсивного спуска.

В задании Match30 описывается основная часть (этап индуктивного перехода) одного из быстрых алгоритмов вычисления значений sp_i(P). Этот алгоритм предложен самими авторами метода КМП, поэтому он обычно называется классическим алгоритмом препроцессинга по методу КМП. Заметим, что в этой же подгруппе заданий описывается и другой вариант быстрого вычисления sp_i(P), базирующийся на основном препроцессинге.

При использовании в качестве языка программирования языка Python модуль PT4Load запускает среду IDLE для выбранной версии языка и сразу загружает в нее программу-заготовку для выбранного задания. Приведем вид этой заготовки для задания Match30 (она сохраняется в файле Match30.pyw):

    # -*- coding: cp1251 -*-
    from pt4 import *
    task("Match30")

Как и заготовки для других языков, данная заготовка обеспечивает подключение к программе специального модуля pt4 с реализациями дополнительных функций задачника и вызов функции task, выполняющей инициализацию указанного задания. Для запуска программы на выполнение достаточно нажать клавишу [F5].

В результате на экране появятся два новых окна: окно Python Shell, в котором «протоколируется» процесс выполнения программ, запущенных из среды IDLE, и окно задачника. Ниже приводится окно задачника:

Как и для других языков, запуск заготовки с заданием считается ознакомительным, так как при этом не выполняются операции ввода-вывода. Заметим, что при закрытии окна задачника активным становится окно Python Shell; для перехода к окну с текстом редактируемой программы проще всего нажать клавиатурную комбинацию [Alt]+[Tab] (можно также выполнить щелчок мышью на окне с текстом программы).

Поскольку язык Python является языком с динамической типизацией (любая переменная может содержать данные любого типа), в реализации задачника для этого языка предусмотрена универсальная функция ввода get, возвращающая очередной элемент исходных данных независимо от его типа. Имеется также универсальная функция вывода put, позволяющая выводить любое количество данных любого типа. При реализации алгоритма, приведенного в формулировке задания, необходимо учесть, что символы в строках на языке Python индексируются от 0, и аналогичным образом индексируются элементы в списках (списки удобно использовать для хранения исходных значений sp_i(P)). Применяя указанные функции ввода-вывода и учитывая особенности, связанные с индексацией, получаем следующий вариант решения:

    # -*- coding: cp1251 -*-
    from pt4 import *
    task("Match30")
    P = get()
    k = get()
    sp = k*[0]
    for i in range(k):
        sp[i] = get()
    x = P[k]
    v = sp[k-1]
    res = 0
    cnt = 0
    while P[v] != x and v > 0:
        cnt += 1
        v = sp[v-1]
    cnt += 2
    if P[v] == x:
        res = v+1
    put(res, cnt)

В этом варианте счетчик сравнений символов увеличивается на 1 на каждой итерации цикла и, кроме того, увеличивается на 2 после выхода из него (учитывается сравнение, выполненное при выходе из цикла, и сравнение, выполненное в условном операторе). При запуске данного варианта решения будет выведено сообщение об успешном тестовом испытании.

Примечание. Нетрудно заметить, что в приведенном алгоритме минимальное число сравнений символов будет равно 2, причем в этом случае будет дважды сравниваться одна и та же пара символов (P[v] и x). Число сравнений символов можно уменьшить на 1, если использовать тот факт, что вычисления сложных логических выражений в языке Python, как и в других современных языках, выполняется по сокращенной схеме, и изменить приведенный в задании алгоритм:

    while v > 0 and P[v] != x:
        v = sp[v-1]
    if v > 0 or P[v] == x:
        res = v+1

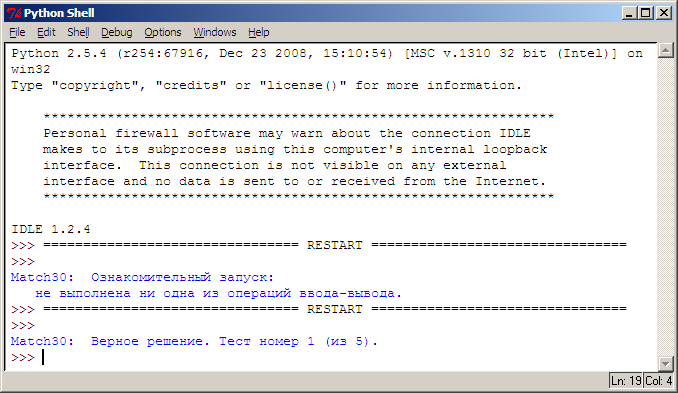
В данном варианте выход из цикла возможен в двух ситуациях: v == 0 и P[v] == x. В первом случае дополнительное сравнение P[v] и x не производится, однако это сравнение выполняется в условном операторе, поскольку первая часть условия (v > 0) является ложной. Во втором случае при выходе из цикла сравнение P[v] и x выполняется, однако при этом v будет больше нуля, и поэтому в условном операторе уже первая часть условия будет истинной, и еще одно сравнение P[v] и x не потребуется. Таким образом, в любом случае число сравнений символов в данной модификации алгоритма будет на 1 меньше, чем число сравнений в алгоритме, описанном в задании Match30. Впрочем, в модифицированном алгоритме требуется выполнять дополнительные сравнения для числовой переменной v, поэтому с практической точки зрения данные алгоритмы имеют одинаковую эффективность. Заметим, что если при выполнении задания использовать приведенную модификацию алгоритма и правильно вычислять число сравнений символов, которое в ней выполняется, то задачник будет выводить сообщение об ошибочном решении, так как найденное число сравнений всегда будет на 1 меньше требуемого.

Сообщения обо всех результатах тестовых испытаний программы протоколируются в окне Python Shell и остаются доступными даже при закрытии окна задачника. В качестве примера приведем вид окна Python Shell после двух описанных выше запусков программы:

При выполнении программы можно выводить в окно Python Shell и другую информацию, используя стандартные средства языка Python. Кроме того, можно использовать отладочные средства задачника, доступные для любых языков, — функции show и show_line; в этом случае информация будет выводиться в специальном разделе отладки окна задачника.

Используем отладочные средства задачника для дополнительного исследования задания: найдем количество сравнений символов, которое требуется для определения значения sp_k+1(P) с помощью наивного алгоритма, выполняющего перебор всех собственных суффиксов строки P[1..k + 1] и их посимвольное сравнение с соответствующими префиксами P. Для этого добавим в конец программы следующий фрагмент:

    cnt = 0
    r = range(k)
    r.reverse()
    for j in r:
        res = j+1
        for i in range(j+1):
            cnt += 1
            if P[i] != P[k-j+i]:
                res = 0
                break
        if res > 0:
            break
    show_line(res)
    show_line("Количество сравнений: " + str(cnt))

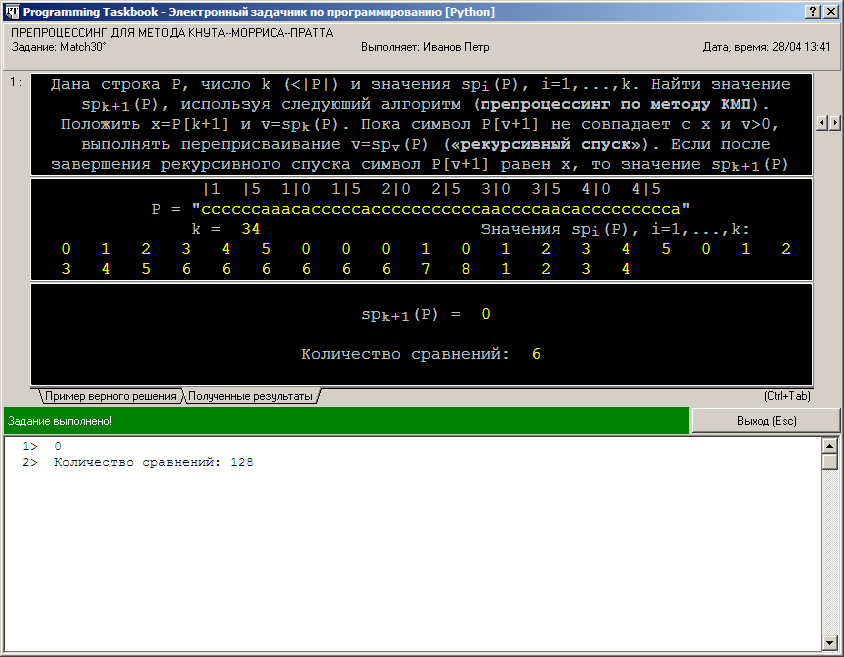
В данном фрагменте последовательно анализируются все собственные суффиксы строки P[1..k + 1] (начиная от суффикса максимальной длины k до суффикса минимальной длины 1). Длина анализируемого суффикса (равная j+1) записывается в переменную res, после чего запускается цикл по i, выполняющий посимвольное сравнение данного суффикса и префикса строки P такой же длины. При обнаружении несовпадающих символов проверка текущего суффикса немедленно прекращается, и начинается анализ следующего суффикса (меньшей длины). Если же анализируемый суффикс совпадает с префиксом, то его длина является искомым значением sp_k+1(P), поэтому происходит немедленный выход из внешнего цикла (по j).

Для проверки полученных результатов в разделе отладки выводится найденное значение sp_k+1(P) и количество сравнений символов, потребовавшееся для его нахождения (снабженное соответствующим комментарием). Следует обратить внимание на то, что в варианте функций show и show_line для языка Python для добавления комментария перед выводимым значением следует сформировать строку, содержащую этот комментарий вместе с самим значением (преобразованным функцией str к своему строковому представлению).

Естественно ожидать, что количество сравнений при подобной реализации алгоритма нахождения sp_k+1(P) будет существенно большим, чем в случае быстрого алгоритма. Несколько запусков полученной программы позволяют наглядно в этом убедиться. Особенно большая разница в числе сравнений будет достигаться для значений sp_k+1(P), равных 0:

Разработка сайта:
М. Э. Абрамян, В. Н. Брагилевский

Последнее обновление:
01.01.2024