Завершающая подгруппа группы Align посвящена алгоритмам, связанным с подпоследовательностями символов в строках. В первом задании этой подгруппы (Align66) вводится понятие подпоследовательности строки и рассматривается задача поиска данной подпоследовательности, допускающая простое решение за линейное время. Остальные задания посвящены существенно более сложной задаче нахождения наибольшей общей подпоследовательности (longest common subsequence — LCS) нескольких строк. В заданиях Align67–69 задача поиска LCS для двух строк сводится к задаче глобального выравнивания с использованием специально подобранной матрицы оценок. Полученный алгоритм ничем, по существу, не отличается от ранее рассмотренных алгоритмов, включающих этапы восходящей рекурсии и обратного прохода (см. примеры выполнения заданий Align31 и Align35). В заданиях Align70–80 рассматривается другой подход к решению задачи об LCS (комбинаторный алгоритм поиска LCS), основанный на предварительном нахождении наибольшей возрастающей подпоследовательности (longest increasing subsequence — LIS) некоторого вспомогательного набора чисел. Рассматривается эффективный алгоритм нахождения LIS, основанный на построении наименьшего покрытия невозрастающими подпоследовательностями с применением алгоритма бинарного поиска (Align70–74). В трех заключительных заданиях (Align78–80) приводится модификация комбинаторного алгоритма, позволяющая находить LCS для трех строк (эта модификация может быть обобщена и на случай большего числа строк).

В данном примере мы рассмотрим вводное задание данной подгруппы, посвященное поиску подпоследовательности.

Align66°. Даны строки P и T (|P| < |T|). Подпоследовательностью строки T называется строка, составленная из символов строки T, взятых в том порядке, в котором они входят в эту строку (символы, входящие в подпоследовательность, в отличие от символов подстрок, не обязаны располагаться подряд в исходной строке). Просматривая символы строк P и T не более одного раза, проверить, входит ли строка P в качестве подпоследовательности в строку T, и вывести True, если входит, и False в противном случае. Вывести также количество сравнений символов, которое потребовалось для решения задачи. В алгоритме учесть, что если еще не просмотренная часть строки T имеет размер, меньший еще не просмотренной части строки P, то строка P не может быть подпоследовательностью строки T.

Опишем первый вариант алгоритма поиска подпоследовательности P в строке T, не учитывающий замечание, сделанное в конце формулировки задания Align66.

Пусть p и t — позиции текущих символов строк P и T соответственно. В начальный момент p = 1 и t = 1. Пока p ≤ |P| и t ≤ |P|, выполнять следующие действия: если P[p] = T[t], то увеличить p на 1; в любом случае увеличить t на 1. Поскольку на каждом шаге значение t увеличивается, цикл обязательно завершится. Если при завершении цикла окажется, что p > |P|, то это будет означать, что в строке T обнаружены все символы строки P, причем в том же порядке, в котором они располагаются в строке P. Если же при завершении цикла условие p > |P| не выполняется, значит, обнаружить все символы строки P (в том же порядке) в строке T не удалось. Таким образом, за однократный просмотр строк P и T задача будет решена.

Если для выполнения задания Align66 использовать язык C#, то описанный выше алгоритм можно реализовать следующим образом (приведем только текст функции Solve, входящей в класс MyTask; по поводу особенностей выполнения заданий на языке C# см. пример выполнения задания Match73):

    public static void Solve()
    {
        Task("Align66");
        string P = GetString(), T = GetString();
        int p = 1, t = 1, cnt = 0;
        while (p <= P.Length && t <= T.Length)
        {
            cnt++;
            if (P[p-1] == T[t-1])
                p++;
            t++;
        }
        Put(p > P.Length, cnt);
    }

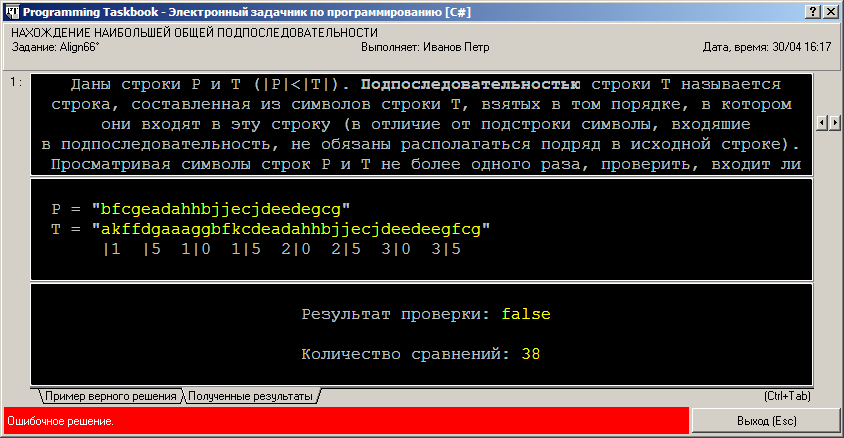
Данная реализация алгоритма отличается от его словесного описания только добавлением счетчика cnt, в котором хранится количество выполненных сравнений символов строк P и T. Учтено также, что на языке C# символы в строках индексируются от 0. Напомним, что для ввода строковых данных в программе на языке C#, использующей задачник, предназначена функция GetString, а для вывода данных любого типа — функция Put.

Разработанный нами вариант алгоритма будет правильно определять, входит ли подпоследовательность P в строку T, однако в случае, когда вхождение отсутствует, число сравнений символов может оказаться больше минимально необходимого. Пример такой ситуации приведен на рисунке:

Заметим, что на вкладке «Пример верного решения» данного окна указывается, что количество сравнений символов равно 18.

Выпишем строки, которые анализировались при указанном тестовом запуске:

    P = "bfcgeadahhbjjecjdeedegcg"
    T = "akffdgaaaggbfkcdeadahhbjjecjdeedeegfcg"
         |1  |5  1|0  1|5  2|0  2|5  3|0  3|5

Для того чтобы убедиться, что данная строка P не входит в качестве подпоследовательности в строку T, нет необходимости просматривать все символы строки T (как это делает наш вариант алгоритма). Анализируя строки P и T, нетрудно определить, что к тому моменту, когда значение счетчика cnt стало равно 18, было обнаружено всего три совпадения для начальных символов строки P: b, f и c (эти совпадения выделены полужирным шрифтом). После анализа 18-й позиции строки T и перехода к позиции номер 19 (эта позиция подчеркнута) в строке T оставалось 20 еще не просмотренных символов, в то время как текущей позицией строки P по-прежнему была позиция 4 (эта позиция также подчеркнута), и, следовательно, еще 21 символ требовал проверки. Понятно, что среди оставшихся 20 символов строки T нельзя обнаружить вхождения 21 оставшегося символа строки P, поэтому на данном этапе алгоритм можно прекращать с выводом результирующего значения false.

Таким образом, анализ символов можно прекращать, как только число еще не просмотренных символов строки P превысит число еще не просмотренных символов строки T (именно эта модификация алгоритма описана в заключительном предложении формулировки задания). Указанные числа равны соответственно |P| – p + 1 и |T| – t + 1; поэтому в заголовок цикла надо добавить условие |P| – p ≤ |T| – t. При этом условие t ≤ |T| в цикле можно не проверять, так как оно является следствием двух других условий: p ≤ |P| и |P| – p ≤ |T| – t.

Примечание. Условие вида |P| – p ≤ |T| – t уже встречалось ранее в задании Match24, посвященном алгоритму Кнута–Морриса–Пратта (см. пример его выполнения).

Получаем окончательный вариант решения:

    public static void Solve()
    {
        Task("Align66");
        string P = GetString(), T = GetString();
        int p = 1, t = 1, cnt = 0;
        while (p <= P.Length && P.Length-p <= T.Length-t)
        {
            cnt++;
            if (P[p-1] == T[t-1])
                p++;
            t++;
        }
        Put(p > P.Length, cnt);
    }

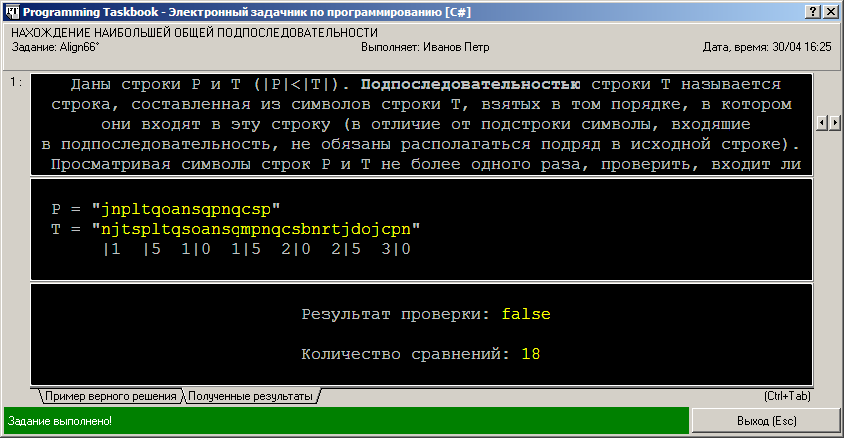
После пяти тестовых запусков будет выведено сообщение о том, что задание выполнено:

Разработка сайта:
М. Э. Абрамян, В. Н. Брагилевский

Последнее обновление:
01.01.2024